Καθώς το κάθε χρώμα υπάρχει σε δύο έδρες, έχουμε: Ρ(Α)= Ρ(Β)= Ρ(Γ)=.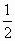

Καθώς δύο χρώματα ταυτόχρονα παίρνω μόνο σε μία έδρα, την τέταρτη, έχουμε Ρ(ΑΒ)=Ρ(ΒΓ)=Ρ(ΑΓ)=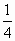. Έτσι τα ενδεχόμενα Α, Β, Γ είναι ανεξάρτητα ανά δύο, για παράδειγμα: P(AB)= P(A)·P(B). Για την από κοινού ανεξαρτησία χρειάζομαι και την σχέση: P(ABΓ)= Ρ(Α)·Ρ(Β)·Ρ(Γ). Αλλά Ρ(ΑΒΓ)= 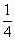και Ρ(Α)·Ρ(Β)·Ρ(Γ)= 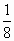. Άρα τα τρία ενδεχόμενα Α, Β και Γ δεν είναι από κοινού ανεξάρτητα.