Έχουμε να εξετάσουμε δύο διαδοχικά διαγωνίσματα. Έστω Α το ενδεχόμενο «ο φοιτητής πήρε στο πρώτο λίαν καλώς» και Β το ενδεχόμενο «ο φοιτητής πήρε στο δεύτερο άριστα». Για την διαμέριση του δειγματικού χώρου Ω πρέπει να πάρουμε τα ενδεχόμενα Η₁: «ο φοιτητής είναι του άριστα», Η₂: «ο φοιτητής είναι του λίαν καλώς» και Η₃: «ο φοιτητής είναι του καλώς». Εάν θέλαμε να βρούμε την αδέσμευτη πιθανότητα του ενδεχομένου Β, θα χρειαζόμασταν τον τύπο της ολικής πιθανότητας με:

Ρ(Η₁)= , Ρ(Η₂)= , Ρ(Η₃)= , Ρ(B|Η₁)= 0.9, Ρ(Η₂)= 0.1 και Ρ(Β|Η₃)= 0.1

Ωστόσο ενδιαφερόμαστε για την δεσμευμένη πιθανότητα του Β δεδομένου του Α, γι’ αυτό βρίσκουμε στην αρχή τις δεσμευμένες πιθανότητες του Η_1, Η₂ και Η₃ δεδομένου του Α, με τον τύπο Bayes. Καθότι Ρ(Α|Η₁)= 0.1, Ρ(Α|Η₂)= 0.7 και Ρ(Α|Η₃)=0.2, έχουμε:

Ρ(Η₁|A)=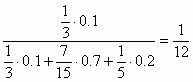

Ρ(Η₂|A)=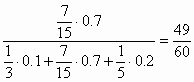

Ρ(Η₃|A)= 1- Ρ(Η₁|A)- Ρ(Η₂|A)=

Έτσι από το βαθμό στο πρώτο διαγώνισμα, είμαστε υποχρεωμένοι να δώσουμε στο φοιτητή νέες πιθανότητες , και για το αν είναι του “άριστα”, του “λίαν καλώς” ή του “καλώς” αντίστοιχα. Τώρα για τον υπολογισμό της πιθανότητας Ρ(Β|Α) χρησιμοποιούμε τον τύπο της ολικής πιθανότητας Ρ(Β|Α)= Ρ(Η₁|A)· Ρ(Β|Η₁Α)+ Ρ(Η₂|A)· Ρ(Β|Η₂Α)+ Ρ(Η₃|A)· Ρ(Β|Η₃Α), όπου στη θέση της πιθανότητας Ρ(Β) και Ρ(Ηi), i= 1, 2, 3 πήραμε τις δεσμευμένες πιθανότητες Ρ(Β|Α) και Ρ(Ηi|Α) και αντί των δεσμευμένων πιθανοτήτων Ρ(Β|Ηi) πήραμε τις δεσμευμένες πιθανότητες Ρ(Β|ΗiΑ) (ελέγξτε την ορθότητα του τύπου αυτού μόνοι σας) . Τότε, θεωρώντας ότι για το φοιτητή μιας ορισμένης κατηγορίας, ο βαθμός του επόμενου διαγωνίσματος δεν εξαρτάται από τον προηγούμενο βαθμό, δηλαδή Ρ(Β|ΗiA)= Ρ(Β|Ηi), παίρνουμε τελικά :

Ρ(Β|Α)= Ρ(Η₁|A)· Ρ(Β|Η₁)+ Ρ(Η₂|A)· Ρ(Β|Η₂)+ Ρ(Η₃|A)· Ρ(Β|Η₃)= · 0.9+ · 0.1+ · 0.1= .