Καθώς το σημείο δεν μπορεί να πέσει έξω από τον κύκλο, ισχύει για την πυκνότητα ότι f(x₁,x₂)= 0 για x₁²+x₂²>R². Για κάθε περιοχή μέσα στον κύκλο (για παράδειγμα τα παραλληλόγραμμο ), η πιθανότητα να πέσει μέσα είναι ανάλογη του εμβαδού της περιοχής (ίση με ΑΔ₁Δ₂, όπου Α συντελεστής αναλογίας). Επομένως από την ιδιότητα της πυκνότητας: f(x₁,x₂)Δ₁Δ₂, έχουμε : f(x₁,x₂) =A για , δηλαδή η πυκνότητα είναι σταθερή στο εσωτερικό του κύκλου. Για να καθορίσουμε τη σταθερά Α χρησιμοποιούμε την σχέση =1. Καθώς f(x₁,x₂) = 0, για x₁²+x₂²>R² ισχύει:

== πΑR² =1,

δηλαδή . Έτσι:

f(x₁,x₂)=

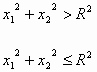
Τώρα εύκολα μπορούμε να βρούμε την περιθώρια πυκνότητα κατανομής της τυχαίας μεταβλητής Χ:

F_X(x) =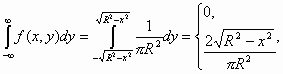

Παρομοίως υπολογίζω και την F_Υ(y).

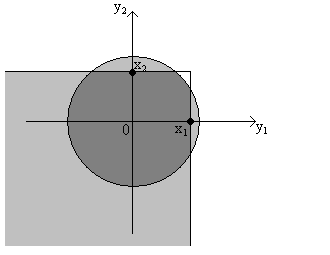
Για την από κοινού συνάρτηση κατανομής F(x₁,x₂), παρατηρούμε ότι από τον ορισμό της πυκνότητας, F(x₁,x₂)= , όπου Δ είναι η τομή του τεταρτημορίου {y₁< x₁, y₂< x₂} και του κύκλου , δηλαδή η F(x₁,x₂) με ακρίβεια μέχρι το συντελεστή συμπίπτει με το εμβαδόν της περιοχής D που φαίνεται στο σχήμα 11 με διπλή γραμμοσκίαση.

Σχήμα 11