Έστω n τυχαίες
μεταβλητές ![]() . Το
διάστημα (Χ1, …, Χn)
ονομάζεται πολυδιάστατη (n-διάστατη)
τυχαία μεταβλητή. Η συνάρτηση κατανομής της
n- διάστατης τυχαίας
μεταβλητής δίνεται από:
. Το
διάστημα (Χ1, …, Χn)
ονομάζεται πολυδιάστατη (n-διάστατη)
τυχαία μεταβλητή. Η συνάρτηση κατανομής της
n- διάστατης τυχαίας
μεταβλητής δίνεται από:
Έστω n=2 , (Χ,Υ)![]() : Εάν Χ,Υ είναι διακριτές με
τιμές {xi} και {yj}
αντίστοιχα, τότε:
: Εάν Χ,Υ είναι διακριτές με
τιμές {xi} και {yj}
αντίστοιχα, τότε:
F(x,y)=![]()
Εάν Χ, Υ συνεχείς, τότε
: F(x,y)=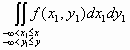 όπου f(x,y) είναι
η από κοινού πυκνότητα κατανομής των Χ και Υ.
όπου f(x,y) είναι
η από κοινού πυκνότητα κατανομής των Χ και Υ.
Η περιθώρια κατανομή της Χ ορίζεται από τον τύπο:
FX(x) =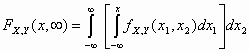 ,
,
και αντίστοιχα για την Υ:
FΥ(y) =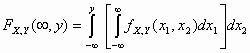 .
.
Η κανονική πολυδιάστατη κατανομή δίνεται από την πυκνότητα :

όπου Α θετικά ορισμένος συμμετρικός τετραγωνικός πίνακας διάστασης
n, A-1 ο αντίστροφος τουΗ δεσμευμένη συνάρτηση κατανομής δίνεται από:
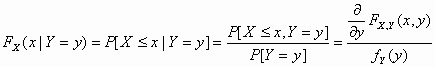 ,
,
και η πυκνότητά της από
:![]() .
.
Οι τυχαίες
μεταβλητές (Χ1, …, Χn)
ονομάζονται ανεξάρτητες
εάν ![]() .
.
Έστω συνάρτηση g(x1,x2)
και δισδιάστατη τυχαία
μεταβλητή (Χ1,X2
). Εάν υπάρχει η
πυκνότητα ![]() η
συνάρτηση κατανομής της Υ δίνεται από τον
τύπο:
η
συνάρτηση κατανομής της Υ δίνεται από τον
τύπο:
![]()
Εάν θέσω όπου
g την συνάρτηση g(x1,x2)= x1+x2 και θεωρήσω τα Χ1,Χ2 ανεξάρτητα τότε παίρνω τον τύπο της συνέλιξης:![]()
Ασκήσεις
Εξετάστε το σχήμα
Bernoulli για n δοκιμές. Ορίστε πολυδιάστατη τυχαία μεταβλητή που να αντιστοιχεί αμφιμονοσήμαντα τα στοιχειώδη ενδεχόμενα με τις τιμές της.
Εξετάστε το αμφιμονοσήμαντο της δισδιάστατης τυχαίας μεταβλητής
(Χ1,X2) με Χ1 το άθροισμα του αποτελέσματος ρίψης δύο ζαριών και Χ2 το άθροισμα των τετραγώνων τους.
Δώστε πολυδιάστατη τυχαία μεταβλητή για το φαινόμενο πτώσης μετεωριτών.
Στο σχήμα Βernoulli με 2 δοκιμές και πιθανότητα επιτυχίας
p, βρείτε την κατανομή του δισδιάστατου τυχαίου διανύσματος (Μ1,Μ2) (βλ. άσκηση 51)
Υποθέτουμε ότι σύμφωνα με την αρχή της γεωμετρικής πιθανότητας πέφτει ένα σημείο τυχαία σε κύκλο ακτίνας
R με κέντρο την αρχή των αξόνων (βλ. άσκηση 12). Βρείτε την πυκνότητα και την συνάρτηση κατανομής τυχαίας μεταβλητής (Χ,Υ) όπου Χ η τετμημένη του σημείου και Υ η τεταγμένη του.
Έστω στα ταμεία της Ολυμπιακής ένας επιβάτης βρίσκει ουρά από Ν άτομα. Προφανώς το Ν είναι διακριτή τυχαία μεταβλητή που παίρνει τιμές 0,1,2,… Εκτός από το μήκος της ουράς Ν εξετάζουμε μία συνεχή τυχαία μεταβλητή Χ, που αντιπροσωπεύει το συνολικό χρόνο που καταναλώνει ο επιβάτης στο ταμείο. Εάν τα διαστήματα μεταξύ προσελεύσεων επιβατών είναι ανεξάρτητα και ακολουθούν την εκθετική κατανομή με παράμετρο λ και η διάρκεια εξυπηρέτησης κάθε επιβάτη στο ταμείο είναι επίσης εκθετικά κατανεμημένη με παράμετρο μ, τότε όπως αποδεικνύεται στη Θεωρία Ουρών Αναμονής, η από κοινού κατανομή των Χ και Ν στη στάσιμη κατάσταση δίνεται από την συνάρτηση
:![]() , με
x>0, i= 0,1,2,…, λ, μ>0,
, με
x>0, i= 0,1,2,…, λ, μ>0, ![]() .
.
Βρείτε την κατανομή του Ν και Χ.
Έστω Χ συνεχής τυχαία μεταβλητή με συνάρτηση κατανομής
F(x) και πυκνότητα f(x). Εξετάζουμε την δισδιάστατη τυχαία μεταβλητή (Χ, Χ) με την ίδια μεταβλητή Χ στις δύο συντεταγμένες της και από κοινού συνάρτηση κατανομής
Βρείτε την δεσμευμένη κατανομή του χρόνου καθυστέρησης του επιβάτη της Ολυμπιακής στο ταμείο Χ (βλ. άσκηση 56) με δεδομένο ότι κατά την προσέλευσή του βρίσκει στην ουρά
i άτομα.Βρείτε τη δεσμευμένη κατανομή του μήκους ουράς Ν στο ταμείο την Ολυμπιακής κατά την προσέλευση επιβάτη, με δεδομένο ότι ο χρόνος καθυστέρησής του στο ταμείο Χ ισούται με x. (βλ. άσκηση 56)
Βρείτε τη δεσμευμένη πυκνότητα κατανομής της τυχαίας μεταβλητής Χ που είναι η τετμημένη του τυχαίου σημείου στην άσκηση 55, με δεδομένο ότι η τεταγμένη Υ ισούται με
y.
Έστω (Χ, Υ) δισδιάστατο κανονικό διάνυσμα με πίνακα συνδιακύμανσης
: A=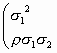
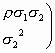 , με σ1,
σ2 >0 , -1<ρ<1
και διάνυσμα μέσων (m1, m2). Βρείτε
τη δεσμευμένη πυκνότητα κατανομής της
τυχαίας μεταβλητής Χ υπό συνθήκη Υ=y.
, με σ1,
σ2 >0 , -1<ρ<1
και διάνυσμα μέσων (m1, m2). Βρείτε
τη δεσμευμένη πυκνότητα κατανομής της
τυχαίας μεταβλητής Χ υπό συνθήκη Υ=y.
Εξετάζουμε το γεωγραφικό πλάτος Χ
1 και το γεωγραφικό μήκος Χ2 του σημείου πτώσης μετεωρίτη στη Γη και το χρόνο Χ3 από την αρχή των παρατηρήσεων έως τη στιγμή της πτώσης (βλ άσκηση 53). Μελετήστε την εξάρτηση των Χ1, Χ2, Χ3.
Εξετάστε ως προς την ανεξαρτησία το πλήθος των επιτυχιών Μ
1, Μ2 στην πρώτη και στη δεύτερη δοκιμή Βernoulli την άσκηση 54.
Δείξτε στην άσκηση 61 ότι οι συντεταγμένες του δισδιάστατου κανονικού τυχαίου διανύσματος είναι ανεξάρτητες εάν και μόνο εάν ρ=0, δηλαδή οι πίνακες Α
-1 και Α είναι διαγώνιοι.
Έστω (Χ
1,Χ2) το δισδιάστατο τυχαίο διάνυσμα, που ακολουθεί την τυποποιημένη κανονική κατανομή. Βρείτε την κατανομή της τυχαίας μεταβλητής
Έστω Χ
1, Χ2 ανεξάρτητες τυχαίες μεταβλητές που ακολουθούν τη Γάμμα κατανομή με παραμέτρους λ, γ1 και λ, γ2 αντίστοιχα. Βρείτε την πυκνότητα κατανομής του αθροίσματος Υ= Χ1+Χ2.