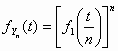
Λύση Άσκησης 93
Ο νόμος των μεγάλων αριθμών, από τον ορισμό του, ισοδυναμεί με την ασθενή σύγκλιση της ακολουθίας των συναρτήσεων κατανομής FY1(x), FY2(x),…, FYn(x),… στην οριακή κατανομή F(x), που αντιστοιχεί στην τυχαία μεταβλητή Υ που παίρνει μια μοναδική τιμή α. Αλλά η Υ έχει σαν χαρακτηριστική συνάρτηση f(t)= eiαt και με βάση το θεώρημα συνέχειας, ικανή και αναγκαία συνθήκη για την ισχύ του νόμου των μεγάλων αριθμών, είναι η σύγκλιση των fYn(x) στην f(t) ομοιόμορφα σε οποιαδήποτε διάστημα [-Τ,Τ]. Παραπέρα, χρησιμοποιώντας ιδιότητες των χαρακτηριστικών συναρτήσεων, έχουμε:
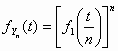
Λογαριθμίζοντας
την fYn(t) (αυτό
μπορεί να γίνει καθώς ![]() ομοιόμορφα σε οποιοδήποτε
διάστημα [-Τ,Τ] και η f(t) δεν
γίνεται μηδέν) παίρνουμε την εξής ικανή και
αναγκαία συνθήκη:
ομοιόμορφα σε οποιοδήποτε
διάστημα [-Τ,Τ] και η f(t) δεν
γίνεται μηδέν) παίρνουμε την εξής ικανή και
αναγκαία συνθήκη:
![]()
ομοιόμορφα σε οποιαδήποτε διάστημα [-Τ,Τ]
. Αυτή η τελευταία συνθήκη με τη σειρά της ισοδηναμεί με τη συνθήκη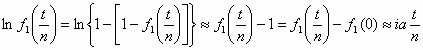
Τέλος θέτοντας ![]() ,
βρίσκουμε ότι ικανή και
αναγκαία συνθήκη για την ισχύ του νόμου των
μεγάλων αριθμών είναι η ύπαρξη του ορίου:
,
βρίσκουμε ότι ικανή και
αναγκαία συνθήκη για την ισχύ του νόμου των
μεγάλων αριθμών είναι η ύπαρξη του ορίου:
![]() ,
,
δηλαδή με άλλα λόγια η ύπαρξη στο μηδέν της παραγώγου
f΄1(0) της χαρακτηριστικής συνάρτησης f΄1(t) και μάλιστα η σταθερά α που εμφανίζεται στο νόμο των μεγάλων αριθμών, ορίζεται μέσω αυτής της παραγώγου από τον τύπο α = -i f΄1(0).