Οριακά Θεωρήματα
1. Ανισότητα
Chebyshev Εάν
υπάρχει DX = ![]() , ισχύει
:
, ισχύει
: ![]() .
.
2. Έστω Χ
1, Χ2,…,Χn,… ακολουθία ανεξάρτητων και ισόνομων τυχαίων μεταβλητών.Αυτή η ακολουθία ικανοποιεί τον (ασθενή) νόμο των μεγάλων αριθμών (ΝΜΑ)
εάν για κάποιο α και οποιοδήποτε ε>0 ισχύει :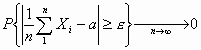
3. Θεώρημα Ν.Μ.Α
Εάν υπάρχουν τα ΕΧ= m και DX = σ2 για την ακολουθία Χ1, Χ2,…,Χn,… των ανεξάρτητων και ισόνομων τυχαίων μεταβλητών, τότε :
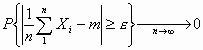
4. Η χαρακτηριστική συνάρτηση της τυχαίας μεταβλητής Χ ορίζεται ως:
. ![]()
με
Ιδιότητες
α)
f(0) = 1, f(t) συνεχήςβ)
fαX+b(t) = fX(αt)eibtγ) Εάν Χ
1, Χ2 ανεξάρτητα τότε f Χ1+Χ2 (t) = f Χ1(t)·f Χ2 (t).δ)
5. Τύπος αντιστροφής χαρακτηριστικής συνάρτησης :
Για κάθε δύο σημεία συνεχείας της συνάρτησης κατανομής F(x) της Χ ισχύει :
F(Χ2)- F(Χ1)
= ![]() .
.
Υπάρχει αμφιμονοσήμαντη αντιστοιχία μεταξύ των συναρτήσεων κατανομής και των χαρακτηριστικών συναρτήσεων.
6. Εάν η ακολουθία συναρτήσεων κατανομής
F1(x),…, Fn(x),… συγκλίνει στη συνάρτηση κατανομής F(x) δηλαδή Fn(x)Fn(x) ![]() F(x).
F(x).
7. Θεώρημα συνεχείας
Ικανή και αναγκαία συνθήκη για την ασθενή σύγκλιση των συναρτήσεων κατανομής
F1(x),…, Fn(x),… στη συνάρτηση F(x) ,( Fn(x)
8. Κεντρικό Οριακό Θεώρημα
Έστω Χ
1, Χ2,…,Χn,… ακολουθία ανεξάρτητων και ισόνομων τυχαίων μεταβλητών με ΕΧn=m και DXn = σ2. Τότε :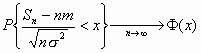 ,
,
με
Sn=
Ασκήσεις
Έστω Χ τυχαία μεταβλητή με πυκνότητα κατανομής. Βρείτε μια εκτίμηση των πιθανοτήτων
Έστω η σειρά
n δοκιμών Bernoulli με πιθανότητα επιτυχίας p. Εάν Μ είναι το πλήθος επιτυχιών στις n δοκιμές, η συχνότητα επιτυχιών ισούται με
Βρείτε τη χαρακτηριστική συνάρτηση της διωνυμικής τυχαίας μεταβλητής
M.
Έστω Χ η εκθετική τυχαία μεταβλητή με παράμετρο λ. Βρείτε τη χαρακτηριστική της συνάρτηση.
Έστω Χ η τυποποιημένη κανονική τυχαία μεταβλητή. Βρείτε τη χαρακτηριστική της συνάρτηση.
Βρείτε τη χαρακτηριστική συνάρτηση της κανονικής τυχαίας μεταβλητής Υ, με μέση τιμή
m και διασπορά σ2.
Βρείτε τη
n-τάξης ροπή της τυχαίας μεταβλητής Χ, που ακολουθεί την εκθετική κατανομή.
Έστω Χ
1, Χ2 ανεξάρτητες τυχαίες μεταβλητές που ακολουθούν την κανονική κατανομή με παραμέτρους m1, σ1 και m2, σ2. Βρείτε την κατανομή του αθροίσματος Υ = Χ1+Χ2.
Έστω Χ
1, Χ2 ανεξάρτητες τυχαίες μεταβλητές που ακολουθούν την κατανομή Poisson με παραμέτρους λ1 και λ2. Βρείτε την κατανομή του αθροίσματος Υ = Χ1+Χ2.
Έστω Χ
1, Χ2,…,Χn,… ακολουθία ανεξάρτητων και ισόνομων τυχαίων μεταβλητών με χαρακτηριστική συνάρτηση fΧn(t)=f1(t). Εξετάζοντας την ακολουθία των αριθμητικών μέσων Υn =
Δείξτε το ολοκληρωτικό θεώρημα
Moivre-Laplace (βλέπε εισαγωγή Κεφαλαίου 3) με τη βοήθεια του κεντρικού οριακού θεωρήματος.
Για τον προσδιορισμό της ταχύτητας
v σωματιδίου κάνουμε n παρατηρήσεις v1, v2,…,vn όπου η i παρατήρηση γίνεται με τυχαίο σφάλμα Χi (δηλαδή vi = v + Χi). Εκτιμήστε την πιθανότητα η μέση παρατηρούμενη ταχύτητα