Έστω η διαφορική εξίσωση πρώτης τάξης

, (1)

όπου οι συναρτήσεις και είναι ορισμένες σ’ ένα ανοιχτό υποσύνολο του .

Ορισμός: Η εξίσωση (1) θα λέγεται ολικού διαφορικού ή ακριβής αν υπάρχει διαφορίσιμη συνάρτηση , ορισμένη στο , τέτοια ώστε

. (2)

Κριτήριο ακρίβειας:

Έστω ότι οι συναρτήσεις και έχουν συνεχείς παραγώγους στο , όπου είναι ένα ανοιχτό και απλά συνεκτικό χωρίο στο . Τότε η (1) είναι ακριβής αν και μόνον αν ισχύει η ισότητα

. (3)

Έστω ότι η εξίσωση (1) είναι ακριβής. Αναζητούμε τότε μια συνάρτηση η οποία ικανοποιεί το παρακάτω σύστημα ισοτήτων

, (4)

. (5)

Ολοκληρώνοντας τις (4) και (5) ως προς και αντίστοιχα, παίρνουμε ότι

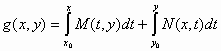, (6)

όπου τυχαίο σημείο του χωρίου . Έτσι, η λύση της (1) δίνεται σε πεπλεγμένη μορφή από την ισότητα

, (7)

όπου είναι μια αυθαίρετη πραγματική σταθερά.

[Επιστροφή στα Περιεχόμενα]

1. [Λύση]

2. [Λύση]

[Επιστροφή στα Περιεχόμενα]