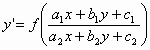ΕΞΙΣΩΣΕΙΣ ΤΗΣ ΜΟΡΦΗΣ

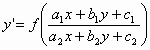, (1)

όπου , , () και , .

Μέθοδος επίλυσης:

Κάνουμε την αλλαγή μεταβλητών

, (2)

όπου και είναι δύο πραγματικές σταθερές οι οποίες θα προσδιοριστούν κατάλληλα στη συνέχεια. Από τις σχέσεις (2) έχουμε

και

.

Παρατηρούμε ότι αν επιλέξουμε και τέτοια ώστε

, (3)

τότε η εξίσωση (1) παίρνει τη μορφή

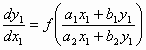, (4)

η οποία είναι ομογενής και επιλύεται κατά τα γνωστά. Φυσικά, το γραμμικό σύστημα (3) έχει λύση αν και μόνον αν

. (5)

Αν τώρα τότε θα υπάρχει τέτοιο ώστε και . Έτσι, στην περίπτωση αυτή η εξίσωση (1) ανάγεται σε χωριζόμενων μεταβλητών με τη βοήθεια του μετασχηματισμού

. (6)

 

[Επιστροφή στα Περιεχόμενα]

 

 

ΑΣΚΗΣΗ:

Να επιλυθεί η διαφορική εξίσωση: . [Λύση]

 

 

[Επιστροφή στα Περιεχόμενα]