ΜΕΘΟΔΟΣ ΤΩΝ ΔΙΑΔΟΧΙΚΩΝ ΠΡΟΣΕΓΓΙΣΕΩΝ
ΤΟΥ
EMILE PICARD
Έστω το πρόβλημα αρχικών τιμών
![]() , (1)
, (1)
![]() , (2)
, (2)
όπου το σημείο
Πρόταση
: Κάθε λύση του προβλήματος αρχικών τιμών (1), (2), είναι επίσης λύση της ολοκληρωτικής εξίσωσης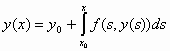 , (3)
, (3)
και αντιστρόφως.
Ως αρχική προσέγγιση της
λύσης ![]() θεωρούμε
μια τυχαία ολοκληρώσιμη συνάρτηση
θεωρούμε
μια τυχαία ολοκληρώσιμη συνάρτηση ![]() ,
το γράφημα της οποίας
διέρχεται από το σημείο
,
το γράφημα της οποίας
διέρχεται από το σημείο ![]() .
Για παράδειγμα, μια καλή
εκλογή της
.
Για παράδειγμα, μια καλή
εκλογή της ![]() είναι
η σταθερή συνάρτηση
είναι
η σταθερή συνάρτηση
![]() . (4)
. (4)
Οι επόμενες προσεγγίσεις ορίζονται από την διαδοχική επίλυση των προβλημάτων αρχικών τιμών
![]() ,
, ![]() (5)
(5)
όπου
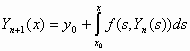 ,
, ![]() (6)
(6)
Κατασκευάζουμε έτσι μια αναδρομική ακολουθία συναρτήσεων
![]() ,
, ![]() ,
,
![]() , ……, (7)
, ……, (7)
οι όροι της οποίας αποτελούν τις κατά
Picard προσεγγίσεις της λύσης![]()
για κάθε
[Επιστροφή στα Περιεχόμενα]
ΑΣΚΗΣΕΙΣ
: Picard προσεγγίσεις![]() ,
, ![]() ,
,
αν ![]() .
[Λύση]
.
[Λύση]
![]() ,
, ![]() ,
,
αν ![]() .
Δείξτε στη συνέχεια ότι
υπάρχει το όριο της
.
Δείξτε στη συνέχεια ότι
υπάρχει το όριο της ![]() καθώς
καθώς
![]() και
ότι είναι λύση του παραπάνω προβλήματος.
[Λύση]
και
ότι είναι λύση του παραπάνω προβλήματος.
[Λύση]
[
Επιστροφή στα Περιεχόμενα]