Έστω η μη-ομογενής γραμμική διαφορική εξίσωση τάξης

. (1)

. (2)

Πρόβλημα: Να βρεθεί μια μερική λύση της (1) υπό την προυπόθεση ότι είναι γνωστές γραμμικώς ανεξάρτητες λύσεις της (2), έστω οι

. (3)

Μέθοδος επίλυσης: Θέτουμε

, (4)

όπου είναι άγνωστες διαφορίσιμες συναρτήσεις οι οποίες απαιτούμε να ικανοποιούν το ακόλουθο γραμμικό σύστημα

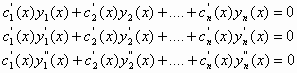
………………………………………………..                                                     (5)

Παρατηρούμε ότι το σύστημα (5) έχει πάντοτε μια μοναδική λύση ως προς τις παραγώγους αφού η ορίζουσά του είναι ακριβώς η ορίζουσα Wronski των γραμμικώς ανεξάρτητων λύσεων της ομογενούς εξίσωσης (2). Έτσι οι άγνωστες συναρτήσεις υπολογίζονται άμεσα με ολοκλήρωση ως προς της μοναδικής λύσης του συστήματος (5) ενώ όλες οι προκύπτουσες σταθερές ολοκλήρωσης μπορούν να παραλειφθούν.

Σημείωση: Η παραπάνω μέθοδος εύρεσης μιας μερικής λύσης της μη-ομογενούς εξίσωσης (1) οφείλεται στον Γάλλο μαθηματικό Joseph L. Lagrange (1713 –1813) και είναι πολύ γενική αφού δεν απαιτεί οι συντελεστές , , της (1) να είναι σταθεροί.

ΑΣΚΗΣΕΙΣ:

Να βρεθεί μια μερική λύση των διαφορικών εξισώσεων:

1. . [Λύση]

2. . [Λύση]

[Επιστροφή στα Περιεχόμενα]