Μια 1-1 και επί συνάρτηση Α ® A λέγεται και μετάθεση του Α.

είναι το σύνολο των μεταθέσεων του Α. Eίναι ομάδα ως προς την σύνθεση συναρτήσεων.

Για φυσικό αριθμό n, S_n συμβολίζει την S_A, όπου A = {1, 2, 3, ... , n}. Η S_n αποτελείται από n! στοιχεία.

Η μετάθεση της S_n που στέλνει το i στο m_i συμβολίζεται με .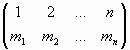

Tα στοιχεία της S₃ είναι :

ρ = , ρ² = , ρ³ = e, μ₁ = , μ₂ = και μ₃ =

Η S₃ ταυτίζεται με τη διεδρική ομάδα D₃, η οποία αποτελείται από όλες τις συμμετρίες του ισόπλευρου τριγώνου. Αν οι κορυφές του τριγώνου ονομαστούν 1, 2, 3, τότε η ρ παριστάνει στροφή 120° γύρω από το κέντρο του τριγώνου, η μ₁ παριστάνει ανάκλαση ως προς την διχοτόμο της γωνίας 1, κ.ο.κ.

Η διεδρική ομάδα D₄, η οποία αποτελείται από όλες τις συμμετρίες του τετραγώνου, είναι υποομάδα της S₄. Αποτελείται από την στροφή 90° γύρω από το κέντρο του τριγώνου ρ = , ρ², ρ³, ρ⁴ = e, δύο ανακλάσεις ως προς τις μεσοκαθέτους μ₁ = , μ₂ = , και δύο ανακλάσεις ως προς τις διαγωνίους δ₁ = , δ₂ = .

11.1. Nα κάνετε τον πίνακα πολλαπλασιασμού της S₃.

Λύση

11.2. Δείξτε ότι η S₃ δεν είναι αβελιανή.

Λύση

11.3. Βρείτε την τάξη των στοιχείων ρ, μ₁ και ρμ₁ της S₃.

Λύση

11.4. Δείξτε ότι η D₄ δεν είναι αβελιανή.

Υπόδειξη

Λύση

11.5. Βρείτε την τάξη όλων των στοιχείων της D₄. Υπολογίστε το ρ²⁷.

Λύση

11.6.Βρείτε όλα τα αριστερά και όλα τα δεξιά σύμπλοκα της υποομάδας Η = <μ₁> της S₃.

Λύση

11.7. Δώστε ένα παραδειγμα υποομάδας Η ομάδας G όπου ισχύει aH = Ha για όλα τα στοιχεία a της G

Λύση

και ένα παράδειγμα όπου δεν ισχύει.

Λύση

11.8. Δείξτε ότι η άσκηση 8.13. δεν ισχύει χωρίς την συνθήκη ab = ba.

Λύση

11.9. Σε αβελιανή ομάδα, αν παραλειφθεί η συνθήκη μκδ( , ) = 1, ισχύει ότι ή διαιρεί την ;

Υπόδειξη

Λύση