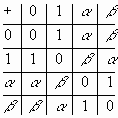
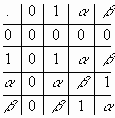
24.4. Σύμφωνα με το θεώρημα 24.2, τα μελη του Ζ2[x] / <f(x)>, όπου f(x) = x2 + x + 1
είναι τα: 0 = <f(x)>, 1 = 1 + <f(x)>, α = x και β = 1 + x+ <f(x)>.
Ακολουθούν οι πίνακες πρόσθεσης και πολλαπλασιασμού.


Από τον πίνακα πολλαπλασιασμού προκύπτει ότι το πηλίκο είναι
αντιμεταθετικός δακτύλιος με μοναδιαίο στοιχείο το 1 και κάθε μη
μηδενικό στοιχείο του είναι μονάδα ( το α έχει αντίστροφο β).
Ετσι ο δακτύλιος Ζ2[x] / <f(x)> είναι σώμα.
f(α) = α2 + α +1 = x2 + x + 1 + <f(x)> = 0.
f(β) = (x + 1)2 + (x + 1) + 1 + <f(x)> = (x2 + 1) + x + <f(x)> = 0.
Eτσι στο Ζ2[x] / <f(x)> το f(x) έχει 2 ρίζες, το α και το β.