

Next: Άσκηση
Up: Άσκηση
Previous: Υπόδειξη
Η διανυσματική εξίσωση τού επιπέδου είναι
Τα διανύσματα θέσης των κορυφών είναι
A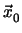 , B
, B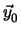 , C
, C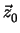 .
Αυτά ικανοποιούν την εξίσωση του επιπέδου, οπότε
Αντικαθιστούμε τις τιμές αυτές στον τύπο του εμβαδού τριγώνου (8)
και μετά από απλές πράξεις, και χρησιμοποιώντας το γεγονός ότι
.
Αυτά ικανοποιούν την εξίσωση του επιπέδου, οπότε
Αντικαθιστούμε τις τιμές αυτές στον τύπο του εμβαδού τριγώνου (8)
και μετά από απλές πράξεις, και χρησιμοποιώντας το γεγονός ότι
|
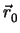
|
2 = (
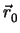 .
. 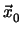
)
2 + (
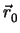 .
. 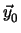
)
2 + (
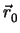 .
. 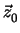
)
2
Aristophanes Dimakis
1999-10-05
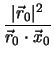 , B =
, B = 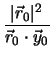 , C =
, C = 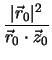 .
.