next up previous
Next: Άσκηση Up: No Title Previous: Λύση

Μετρικές ιδιότητες και συστήματα αναφοράς

Σε κάθε σημείο του χώρο P αντιστοιχούμε ένα διάνυσμα θέσης $ \vec{r}\,$, αν προηγούμενα έχουμε επιλέξει ένα σημείο αναφοράς O. Το σημείο αναφοράς λέγεται αρχή και το διάνυσμα θέσης είναι το $ \vec{r}\,$ = $ \overrightarrow{OP}$.

Τρία γραμμικά ανεξάρτητα διανύσματα, μια βάση του διανυσματικού χώρου, ορίζουν ένα σύστημα αναφοράς με αρχή το O. Συνήθως παίρνουμε τρία μοναδιαία διανύσματα $ \vec{x}_{0}^{}$,$ \vec{y}_{0}^{}$,$ \vec{z}_{0}^{}$ που ορίζουν τρεις άξονες Ox, Oy, Oz.

Ως ένα προς σύστημα αναφοράς έχουμε $ \vec{r}\,$ = x$ \vec{x}_{0}^{}$ + y$ \vec{y}_{0}^{}$ + z$ \vec{z}_{0}^{}$. Οι τριάδα (x, y, z) προσδιορίζει μονοσήμαντα το σημείο P. Οι αριθμοί x, y, z καλούνται συντεταγμένες του σημείου P.

Αν τα διανύσματα $ \vec{x}_{0}^{}$,$ \vec{y}_{0}^{}$,$ \vec{z}_{0}^{}$ είναι ανά δύο ορθογώνια μεταξύ τους το σύστημα αναφοράς καλείται ορθοκανονικό.

Η απόσταση μεταξύ δύο σημείων P1(x1, y1, z1) και P2(x2, y2, z2) στο χώρο ως προς ορθοκανονικό σύστημα αναφοράς είναι

d (P1, P2) = |$\displaystyle \overrightarrow{P_1P_2}$| = $\displaystyle \sqrt{(x_2-x_1)^2+ y_2-y_1)^2+(z_2-z_1)^2}$  .     (7)

Το εμβαδόν ενός τριγώνου με κορυφές τα σημεία P1(x1, y1, z1), P2(x2, y2, z2) και P3(x3, y3, z3) ως προς ορθοκανονικό σύστημα αναφοράς είναι
Εμβ(P1P2P3) = $\displaystyle {1\over 2}$$\displaystyle \sqrt{\left\vert\begin{array}{ccc} y_1 & z_1 & 1 \\ y_2 & z_2 & 1... ...{ccc} x_1 & y_1 & 1 \\ x_2& y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right\vert^2 }$  .     (8)

Όταν τα τρία σημεία κείνται στο Oxy επίπεδο, οπότε z1 = z2 = z3 = 0, παίρνουμε
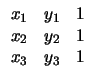
Εμβ(P1P2P3) = $\displaystyle {1\over 2}$ |$\displaystyle \left\vert\vphantom{\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1\end{array}}\right.$$\displaystyle \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1\end{array}}\right\vert$|  .     (9)

Ο όγκος ενός τετραέδρου με κορυφές Pi(xi, yi, zi), i = 1, 2, 3, 4 ως προς ορθοκανονικό σύστημα αναφοράς είναι
Ογκ(P1P2P3P4) = $\displaystyle {1\over 6}$ |$\displaystyle \left\vert\vphantom{ \begin{array}{cccc} x_1&y_1&z_1&1\\ x_2&y_2&z_2&1\\ x_3&y_3&z_3&1\\ x_4&y_4&z_4&1 \end{array}}\right.$$\displaystyle \begin{array}{cccc} x_1&y_1&z_1&1\\ x_2&y_2&z_2&1\\ x_3&y_3&z_3&1\\ x_4&y_4&z_4&1 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cccc} x_1&y_1&z_1&1\\ x_2&y_2&z_2&1\\ x_3&y_3&z_3&1\\ x_4&y_4&z_4&1 \end{array}}\right\vert$|  .     (10)

Ο απλός λόγος τριών σημείων P1, P2, P πάνω σε μια ευθεία είναι
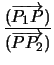(P1P2P) = $\displaystyle {\frac{(\overrightarrow{P_1P})}{(\overrightarrow{PP_2})}}$  ,     (11)

όπου ($ \overrightarrow{P_1P_2}$) είναι το προσημασμένο μήκος του διανύσματος $ \overrightarrow{P_1P_2}$.

Αν έχουμε (P1P2P) = $\lambda$ και (x1, y1, z1),  (x2, y2, z2),  (x, y, z) είναι οι συντεταγμένες των σημείων P1, P2, P αντίστοιχα, τότε

x = $\displaystyle {\frac{x_1+\lambda x_2}{1+\lambda}}$,        y = $\displaystyle {\frac{y_1+\lambda y_2}{1+\lambda}}$,        z = $\displaystyle {\frac{z_1+\lambda z_2}{1+\lambda}}$.     (12)

Αν το σύστημα αναφοράς Oxyz μετατοπισθεί παράλληλα, έτσι ώστε η αρχή των αξόνων να μετακινηθεί στο σημείο O'($ \alpha$,$ \beta$,$ \gamma$), τότε προκύπτει ένα νέο σύστημα αναφοράς O'x'y'z'. Γιά τις συντεταγμένες ενός σημείου στα δύο συστήματα έχουμε

x = $\displaystyle \alpha$ + x',            y = $\displaystyle \beta$ + y',            z = $\displaystyle \gamma$ + z'.     (13)

Στο επίπεδο η αλλαγή συντεταγμένων από ένα ορθογώνιο σε ένα πλαγιγώνιο σύστημα αναφοράς όπως περιγράφεται στο σχήμα

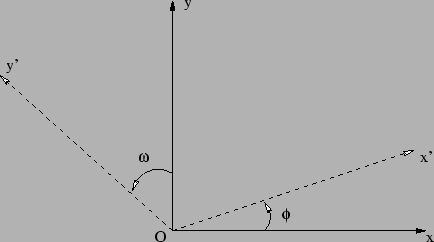
\epsfig{file=thew2.eps, scale=.8}
είναι
x = x'cos$\displaystyle \varphi$ - y'sin$\displaystyle \omega$
y = x'sin$\displaystyle \varphi$ + y'cos$\displaystyle \omega$
.		     (14)


next up previous
Next: Άσκηση Up: No Title Previous: Λύση
Aristophanes Dimakis
1999-10-05