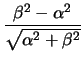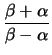

Next: Η ευθεία στο επίπεδο
Up: Άσκηση
Previous: Υπόδειξη
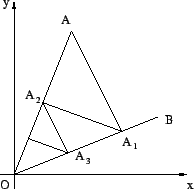
Τα τρίγωνα OAA1,
OA1A2,..., OAn - 1An είναι όμοια γιατί είναι
ορθογώνια και έχουν τη γωνία
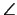 (AOB) κοινή. Συνεπώς έχουμε τις σχέσεις
αναλογίας
(AOB) κοινή. Συνεπώς έχουμε τις σχέσεις
αναλογίας
και συγκρίνοντας παίρνουμε
Από τις παραπάνω σχέσεις είναι προφανές ότι
An - 1An = 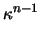 AA1, AA1, |
|
|
|
συνεπώς μένει να υπολογίσουμε το
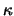 =
= 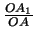 και ΑΑ1.
Από τις συντεταγμένες των σημείων A, B έχουμε
OA = OB =
και ΑΑ1.
Από τις συντεταγμένες των σημείων A, B έχουμε
OA = OB = 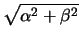 . Επίσης από το εμβαδόν του τριγώνου OAB
έχουμε
. Επίσης από το εμβαδόν του τριγώνου OAB
έχουμε
Εμβ(OAB) = 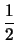 (OB)(AA1) = (OB)(AA1) = 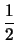 | |  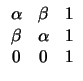
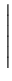 |. |. |
|
|
|
Αντικαθιστώντας παίρνουμε
οπότε
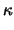 =
= 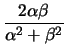 . . |
|
|
|
Bρίσκουμε
| AA1 + A1A2 + ... + An - 1An |
= |
AA1(1 + 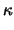 + ... +
+ ... + 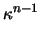 ) ) |
|
| |
= |
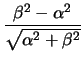 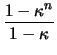 . . |
|
Επειδή
0 < 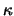 < 1, έχουμε τελικά
< 1, έχουμε τελικά
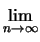 (AA1 + A1A2 + ... + An - 1An) (AA1 + A1A2 + ... + An - 1An) |
= |
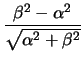 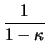 |
|
| |
= |
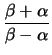 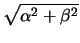 . . |
|


Next: Η ευθεία στο επίπεδο
Up: Άσκηση
Previous: Υπόδειξη
Aristophanes Dimakis
1999-10-05
![]() (AOB) κοινή. Συνεπώς έχουμε τις σχέσεις
αναλογίας
(AOB) κοινή. Συνεπώς έχουμε τις σχέσεις
αναλογίας
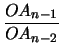 =
= 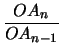 =
= 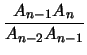 ,
,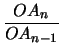 =
= 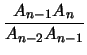 =
= 
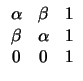
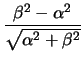 , OA1 =
, OA1 = 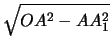 =
= 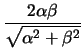 ,
,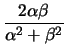 .
.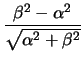
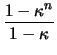 .
.