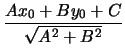

Next: Άσκηση
Up: No Title
Previous: Λύση
Μια ευθεία που παιρνά από το σημείο
P1(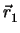 ) και είναι παράλληλη προς
διάνυσμα
) και είναι παράλληλη προς
διάνυσμα 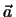 έχει εξίσωση
έχει εξίσωση
ενώ αν παιρνά και από το σημείο
P2(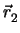 ) έχει εξίσωση
) έχει εξίσωση
όπου
t 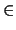
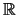 . Σε συντεταγμένες οι παραπάνω εξισώσεις γίνονται
. Σε συντεταγμένες οι παραπάνω εξισώσεις γίνονται
| x |
= |
x1 + t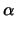 |
| y |
= |
y1 + t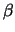 |
ή 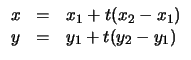 , , |
|
|
(17) |
με
t 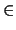
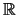 . Σε αναλυτική μορφή οι εξίσωση της ευθείας στο επίπεδο είναι
. Σε αναλυτική μορφή οι εξίσωση της ευθείας στο επίπεδο είναι
Οι εξισώσεις αυτές έχουν τη γενική μορφή
Ax + By + C = 0, (A, B) 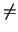 (0, 0).
(0, 0). |
|
|
(19) |
Η κλίση 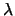 μιας ευθείας είναι η εφαπτομένη της γωνίας που σχηματίζει
η ευθεία με τον άξονα Ox. Συνεπώς η ευθεία που έχει κλίση
μιας ευθείας είναι η εφαπτομένη της γωνίας που σχηματίζει
η ευθεία με τον άξονα Ox. Συνεπώς η ευθεία που έχει κλίση 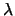 και περνάει
από το σημείο (x0, y0) είναι
και περνάει
από το σημείο (x0, y0) είναι
y - y0 = 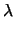 (x - x0). (x - x0). |
|
|
(20) |
Δυο ευθείες είναι κάθετες αν το γινόμενο των κλίσεων
τους είναι -1, δηλ.
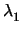
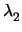 = - 1.
= - 1.
Το διάνυσμα (B, - A) είναι παράλληλο προς την ευθεία, ενώ το διάνυσμα (A, B)
είναι κάθετο προς αυτήν.
Οι δύο εξισώσεις
| A1x + B1y + C1 = 0, A2x + B2y + C2 = 0 |
|
|
(21) |
παριστάνουν παράλληλες ευθείες, αν
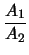 =
= 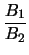 , , |
|
|
(22) |
ενώ παριστάνουν την ίδια ευθεία αν
Η σχετική θέση τριών ευθειών
Aix + Biy + Ci = 0, i = 1, 2, 3 εξαρτάται από τις
τάξεις των δύο πινάκων
Έχουμε τις εξής περιπτώσεις:
α)
r(D) = 1, r(E) = 1. Οι τρείς ευθείες συμπίπτουν.
β)
r(D) = 1, r(E) = 2. Οι τρείς ευθείες είναι παράλληλες.
γ)
r(D) = 2, r(E) = 2. Οι τρείς ευθείς περνούν από το ίδιο σημείο.
δ)
r(D) = 2, r(E) = 3. Οι τρείς ευθείες σχηματίζουν τρίπλευρο.
Επίπεδη δέσμη ευθειών είναι το σύνολο των ευθειών του επιπέδου που
διέρχονται από ένα σημείο ή είναι παράλληλες μεταξύ τους.
Αν
Aix + Biy + Ci = 0, i = 1, 2 είναι δυο ευθείες της δέσμης τότε κάθε αλλή ευθεία
που ανήκει στη δέσμη που ορίζουν αυτές έχει εξίσωση
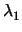 (A1x + B1y + C1) + (A1x + B1y + C1) + 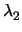 (A2x + B2y + C2) = 0. (A2x + B2y + C2) = 0. |
|
|
(24) |
Μια ευθεία Ax + By + C = 0 χωρίζει το επίπεδο σ'ένα θετικό και ένα αρνητικό
ημιεπίπεδο. Ως θετικό ημιεπίπεδο ορίζεται εκείνο στο οποίο η παράσταση
Ax + By + C παίρνει θετική τιμή. Το κάθετο διάνυσμα (A, B) δείχνει προς το θετικό
ημιεπίπεδο.
Ο τύπος
d = 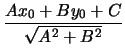 |
|
|
(25) |
δίνει την προσημασμένη απόσταση του σημείου
P0(x0, y0) από την ευθεία
Ax + By + C = 0. Η τιμή της d είναι αρνητική αν το σημείο βρίσκεται στο αρνητικο
ημιεπίπεδο.


Next: Άσκηση
Up: No Title
Previous: Λύση
Aristophanes Dimakis
1999-10-05
![]() ) και είναι παράλληλη προς
διάνυσμα
) και είναι παράλληλη προς
διάνυσμα ![]() έχει εξίσωση
έχει εξίσωση
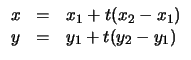 ,
,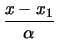 =
= 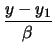 ή
ή 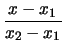 =
= 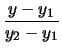 .
.