

Next: Ο Κύκλος
Up: Άσκηση
Previous: Υπόδειξη
Το διάνυσμα
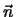 = (1, - 3, - 1) είναι κάθετο στο επίπεδο (E) και δείχνει
προς τον θετικό ημίχωρο του (E). Το εσωτερικό γινόμενο
= (1, - 3, - 1) είναι κάθετο στο επίπεδο (E) και δείχνει
προς τον θετικό ημίχωρο του (E). Το εσωτερικό γινόμενο
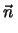 .
. 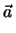
= - 3 < 0
είναι αρνητικό, πράγμα που σημαίνει ότι η γωνία μεταξύ των 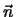 και
και
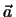 είναι αμβλεία και συνεπώς το
είναι αμβλεία και συνεπώς το 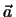 δείχνει προς τον αρνητικό ημίχωρο
του (E). Άρα η προσημασμένη απόσταση των επιπέδων είναι
-
δείχνει προς τον αρνητικό ημίχωρο
του (E). Άρα η προσημασμένη απόσταση των επιπέδων είναι
- 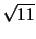 .
.
Η απόσταση τυχόντος σημείου P(x, y, z) του ζητούμενου επιπέδου από το (E) είναι
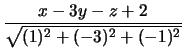
,
συνεπώς
είναι η εξίσωση του ζητούμενου επιπέδου.
Aristophanes Dimakis
1999-10-05
![]() = (1, - 3, - 1) είναι κάθετο στο επίπεδο (E) και δείχνει
προς τον θετικό ημίχωρο του (E). Το εσωτερικό γινόμενο
= (1, - 3, - 1) είναι κάθετο στο επίπεδο (E) και δείχνει
προς τον θετικό ημίχωρο του (E). Το εσωτερικό γινόμενο
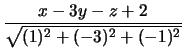 ,
,
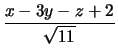 = -
= -