

Next: Άσκηση
Up: No Title
Previous: Λύση
Η περιφέρεια κύκλου είναι ο γεωμετρικός τόπος των σημείων του επιπέδου που
απέχουν σταθερή απόσταση R από ένα ορισμένο σημείο K, το κέντρο
του κύκλου. Αν P σημείο της περιφέρειας τότε
|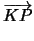 | = R. | = R. |
|
|
(38) |
Αν
K(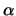 ,
,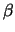 ) και P(x, y) τότε η εξίσωση της περιφέρειας είναι
) και P(x, y) τότε η εξίσωση της περιφέρειας είναι
(x - 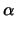 )2 + (y - )2 + (y - 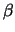 )2 = R2. )2 = R2. |
|
|
(39) |
Εν γένει η εξίσωση
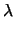 (x2 + y2) + Ax + By + C = 0 (x2 + y2) + Ax + By + C = 0 |
|
|
(40) |
παριστάνει περιφέρεια κύκλου. Γιά 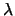 = 1 το κέντρο της περιφέρειας
είναι το σημείο
K(- A/2, - B/2) και η ακτίνα της είναι
R =
= 1 το κέντρο της περιφέρειας
είναι το σημείο
K(- A/2, - B/2) και η ακτίνα της είναι
R = 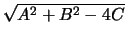 /2.
/2.
Η εξίσωση της περιφέρειας που διέρχεται από τρία δοθέντα σημεία
Pi(xi, yi),
i = 1, 2, 3 είναι
Σε μια περιφέρεια με εξίσωση (39) και ένα σημείο
P0(x0, y0)
αντιστοιχεί η πολική ευθεία με εξίσωση
(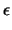 ) : (x0 - ) : (x0 - 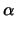 )(x - )(x - 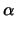 ) + (y0 - ) + (y0 - 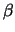 )(y - )(y - 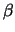 ) = R2. ) = R2. |
|
|
(42) |
Το σημείο P0 είναι ο πόλος της ευθείας
(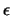 ). Όταν ο πόλος
βρίσκεται πάνω στην περιφέρεια, η πολική ευθεία είναι η εφαπτομένη του κύκλου
στον πόλο.
). Όταν ο πόλος
βρίσκεται πάνω στην περιφέρεια, η πολική ευθεία είναι η εφαπτομένη του κύκλου
στον πόλο.
Η δύναμη σημείου
P(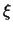 ,
,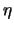 ) ως προς κύκλο (39) είναι το μέγεθος
) ως προς κύκλο (39) είναι το μέγεθος
(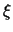 -
- 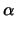 )2 + ( )2 + (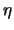 -
- 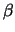 )2 - R2. )2 - R2. |
|
|
(43) |
Ο γεωμετρικός τόπος των σημείων του επιπέδου που έχουν την ίδια δύναμη ως πρός
δύο κύκλους είναι ευθεία γραμμή και λέγεται ριζικός άξονας των δύο περιφερειών.
Οι τρείς ριζικοί άξονες τριών περιφερειών, αν ληφθούν ανα δύο, διέρχονται από το
ίδιο σημείο που καλείται ριζικό κέντρο των τριών περιφερειών.
Δεδομένων δύο περιφερειών
x2 + y2 + Aix + Biy + Ci = 0, i = 1, 2 το σύνολο των
περιφερειών με εξίσωση
x2 + y2 + A1x + B1y + C1 + 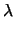 (x2 + y2 + A2x + B2y + C2) = 0 (x2 + y2 + A2x + B2y + C2) = 0 |
|
|
(44) |
για
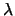
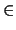
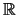 καλείται δέσμη περιφερειών.
καλείται δέσμη περιφερειών.
Δύο παραμετρικές μορφές της περιφέρειας (39) είναι
x = 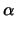 + Rcos
+ Rcos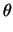 , y = , y = 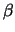 + Rsin
+ Rsin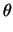 , , 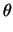
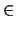 [0, 2
[0, 2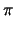 ], ], |
|
|
(45) |


Next: Άσκηση
Up: No Title
Previous: Λύση
Aristophanes Dimakis
1999-10-05
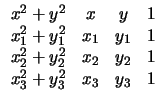
![]() ,
,![]() ) ως προς κύκλο (39) είναι το μέγεθος
) ως προς κύκλο (39) είναι το μέγεθος
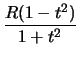 , y =
, y = 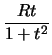 , t
, t