


Next: 'Ασκηση 3
Up: 'Ασκηση 2
Previous: Υπόδειξη
Λύση
Για 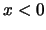 καθώς επίσης και για
καθώς επίσης και για 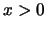 η συνάρτηση μας είναι συνεχής (γιατί;).
Για να είναι συνεχής στο
η συνάρτηση μας είναι συνεχής (γιατί;).
Για να είναι συνεχής στο 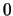 πρέπει
πρέπει
'Ομως
και
Άρα η συνάρτηση είναι συνεχής από αριστερά στο 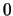 και όχι από δεξιά, οπότε δεν
είναι συνεχής στο
και όχι από δεξιά, οπότε δεν
είναι συνεχής στο  .
'Εχει μάλιστα ασυνέχεια α' είδους.
.
'Εχει μάλιστα ασυνέχεια α' είδους.
'Ασκηση 2
Υπόδειξη
Antonis Tsolomitis
1999-11-11