


Next: Κυρτές και κοίλες συναρτήσεις.
Up: Παραγώγιση συναρτήσεων
Previous: Μονότονες συναρτήσεις
Ορισμός 62
'Εστω συνάρτηση
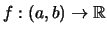
.
Αν υπάρχει
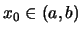
τέτοιο
ώστε:
(i)
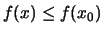 για κάθε
για κάθε 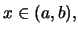 τότε λέμε ότι η συνάρτηση
τότε λέμε ότι η συνάρτηση  έχει μέγιστο
στο σημείο
έχει μέγιστο
στο σημείο 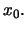 Γράφουμε
Γράφουμε
(ii)
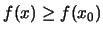 για κάθε
για κάθε 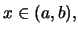 τότε λέμε ότι η συνάρτηση
τότε λέμε ότι η συνάρτηση  έχει ελάχιστο στο σημείο
έχει ελάχιστο στο σημείο 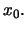 Γράφουμε
Γράφουμε
Δεν είναι απαραίτητο μια συνάρτηση να έχει μέγιστο ή ελάχιστο.
Ορισμός 63
'Εστω συνάρτηση
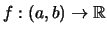
.
Αν υπάρχει
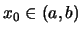
τέτοιο
ώστε
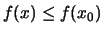
ή
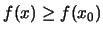
για τα
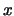
που είναι σε κάποια περιοχή του
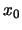
(δηλαδή σύνολο της μορφής
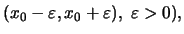
τότε λέμε ότι η συνάρτηση

έχει τοπικό μέγιστο ή τοπικό ελάχιστο αντίστοιχα, στο σημείο
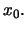
Θεώρημα 64
(Fermat) 'Εστω συνάρτηση
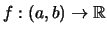
.
Αν έχει
τοπικό ακρότατο στο σημείο
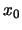
και είναι παραγωγίσιμη στο σημείο αυτό, τότε
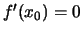
.
Γεωμετρική ερμηνεία. Αν το 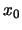 είναι σημείο τοπικού ακροτάτου μιας
παραγωγίσιμης συνάρτησης, τότε η εφαπτομένη του γραφήματός της στο
είναι σημείο τοπικού ακροτάτου μιας
παραγωγίσιμης συνάρτησης, τότε η εφαπτομένη του γραφήματός της στο 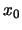 είναι
οριζόντια.
είναι
οριζόντια.
Θεώρημα 65
'Εστω παραγωγίσιμη συνάρτηση
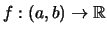
με
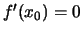
για την
οποία υπάρχει η δεύτερη παράγωγος στο
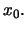
Αν
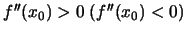
το
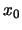
είναι θέση τοπικού ελαχίστου (μεγίστου).
Antonis Tsolomitis
1999-11-11
![]() για κάθε
για κάθε ![]() τότε λέμε ότι η συνάρτηση
τότε λέμε ότι η συνάρτηση ![]() έχει μέγιστο
στο σημείο
έχει μέγιστο
στο σημείο ![]() Γράφουμε
Γράφουμε ![]() για κάθε
για κάθε ![]() τότε λέμε ότι η συνάρτηση
τότε λέμε ότι η συνάρτηση ![]() έχει ελάχιστο στο σημείο
έχει ελάχιστο στο σημείο ![]() Γράφουμε
Γράφουμε
![]() για κάθε
για κάθε ![]() τότε λέμε ότι η συνάρτηση
τότε λέμε ότι η συνάρτηση ![]() έχει μέγιστο
στο σημείο
έχει μέγιστο
στο σημείο ![]() Γράφουμε
Γράφουμε ![]() για κάθε
για κάθε ![]() τότε λέμε ότι η συνάρτηση
τότε λέμε ότι η συνάρτηση ![]() έχει ελάχιστο στο σημείο
έχει ελάχιστο στο σημείο ![]() Γράφουμε
Γράφουμε
![]() είναι σημείο τοπικού ακροτάτου μιας
παραγωγίσιμης συνάρτησης, τότε η εφαπτομένη του γραφήματός της στο
είναι σημείο τοπικού ακροτάτου μιας
παραγωγίσιμης συνάρτησης, τότε η εφαπτομένη του γραφήματός της στο ![]() είναι
οριζόντια.
είναι
οριζόντια.