


Next: 'Ασκηση 6
Up: 'Ασκηση 5
Previous: Υπόδειξη
Λύση
'Εχουμε ήδη δει στην 'Ασκηση 3 ότι για κάθε
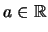 η συνάρτηση είναι συνεχής στο
η συνάρτηση είναι συνεχής στο 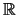 .
Για
.
Για 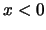 καθώς επίσης και για
καθώς επίσης και για 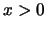 η συνάρτηση μας είναι προφανώς παραγωγίσιμη.
Για να είναι παραγωγίσιμη και στο
η συνάρτηση μας είναι προφανώς παραγωγίσιμη.
Για να είναι παραγωγίσιμη και στο 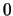 πρέπει να υπάρχει το όριο
πρέπει να υπάρχει το όριο
Επειδή
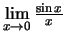 έχουμε
έχουμε
και
Άρα για 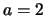 η συνάρτηση είναι παραγωγίσιμη στο
η συνάρτηση είναι παραγωγίσιμη στο 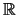 .
.
'Ασκηση 5
Υπόδειξη
Antonis Tsolomitis
1999-11-11