


Next: 'Ασκηση 7
Up: 'Ασκηση 6
Previous: Υπόδειξη
Λύση
Επειδή η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο ![$[0,1]$](img516.gif) θα είναι και συνεχής σ' αυτό. Σύμφωνα
με γνωστό θεώρημα θα έχει ελάχιστο στο διάστημα
θα είναι και συνεχής σ' αυτό. Σύμφωνα
με γνωστό θεώρημα θα έχει ελάχιστο στο διάστημα ![$[0,1]$](img516.gif) .
Αρκεί να δείξουμε ότι δεν
μπορεί να είναι το
.
Αρκεί να δείξουμε ότι δεν
μπορεί να είναι το 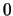 ή το
ή το 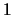 .
'Εστω ότι το
.
'Εστω ότι το 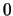 είναι ελάχιστο, τότε
είναι ελάχιστο, τότε
και άρα
Παίρνοντας
όρια στη ανισότητα, από τον ορισμό της παραγώγου στο 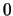 και από γνωστή ιδιότητα
των ορίων, έχουμε ότι
και από γνωστή ιδιότητα
των ορίων, έχουμε ότι
Η σχέση αυτή
έρχεται σε αντίθεση με την υπόθεση ότι 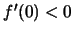 .
'Ομοια απορρίπτουμε και την
περίπτωση το
.
'Ομοια απορρίπτουμε και την
περίπτωση το 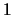 να είναι ελάχιστο.
να είναι ελάχιστο.
'Ασκηση 6
Υπόδειξη
Antonis Tsolomitis
1999-11-11