Λύση

'Εστω

$$a_n = \frac {x}{n} \;\; \hbox{και} \;\; b_n = \frac{1}{n}.$$

Τότε, λόγω της άσκησης 1

$$\lim\limits_{n \to \infty}a_n = \lim \limits_{n\to \infty}b_n=0.$$

Επίσης

$$\lim\limits_{n \to \infty} \frac{a_n}{b_n}=\lim\limits_{n \to \infty} x = x.$$

Τo συμπέρασμα που βγαίνει είναι ότι δεν μπορούμε να αποφανθούμε για την τιμή του ορίου

$$\lim\limits_{n\to\infty}\frac{a_n}{b_n}$$

στη περίπτωση που 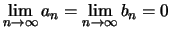$\lim\limits_{n \to \infty}a_n = \lim\limits_{n \to \infty} b_n = 0$ όπως έχουμε δει σε άλλες περιπτώσεις.

'Ασκηση 6 Υπόδειξη