


Next: 'Ασκηση 12
Up: 'Ασκηση 11
Previous: Υπόδειξη
Λύση
Αν 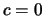 τότε προφανώς η ακολουθία μας είναι η μηδενική.
τότε προφανώς η ακολουθία μας είναι η μηδενική.
'Εστω 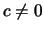 .
Τότε
.
Τότε
και άρα
'Αρα η ακολουθία 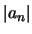 είναι
φθίνουσα (από κάποιο δείκτη και μετά) και φραγμένη (θετικών όρων), οπότε, σύμφωνα
με γνωστό θεώρημα συγκλίνει, έστω στο
είναι
φθίνουσα (από κάποιο δείκτη και μετά) και φραγμένη (θετικών όρων), οπότε, σύμφωνα
με γνωστό θεώρημα συγκλίνει, έστω στο 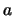 .
Από τη σχέση
.
Από τη σχέση
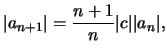 παίρνοντας όρια έχουμε
παίρνοντας όρια έχουμε 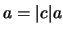 και άρα
και άρα 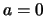 .
Αφού η
.
Αφού η 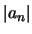 είναι
μηδενική και η
είναι
μηδενική και η 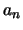 θα είναι μηδενική (βλέπε άσκηση 4).
θα είναι μηδενική (βλέπε άσκηση 4).
'Ασκηση 11
Υπόδειξη
Antonis Tsolomitis
1999-11-11
![]() .
Τότε
.
Τότε 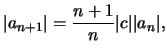 παίρνοντας όρια έχουμε
παίρνοντας όρια έχουμε