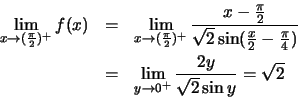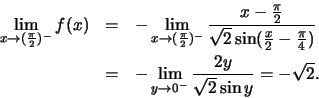Next: 'Ασκηση 4
Up: 'Ασκηση 3
Previous: Υπόδειξη
Λύση
Χρησιμοποιώντας τις ταυτότητες
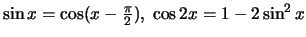 έχουμε ότι
έχουμε ότι
και άρα
Λόγω της μορφής της
συνάρτησης βρίσκουμε τα πλευρικά όρια χρησιμοποιώντας το όριο
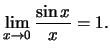 Είναι
Είναι
και
Τα πλευρικά όρια είναι διαφορετικά και άρα σύμφωνα με γνωστό θεώρημα
δεν υπάρχει το όριο.
'Ασκηση 3
Υπόδειξη
Antonis Tsolomitis
1999-11-11
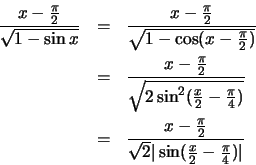
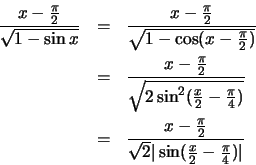
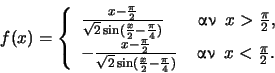
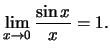 Είναι
Είναι