Έστω URⁿ , f: U® R μια διαφορίσιμη συνάρτηση και C: [a, b]® U μια καμπύλη. Τότε η παράγωγος της συνάρτησης t® f(C(t)) δίνεται από τον τύπο

ο οποίος ονομάζεται κανόνας της αλυσίδας.

Αν C(t) = (x₁(t),..., x_n(t)) τότε ο κανόνας της αλυσίδας παίρνει την μορφή

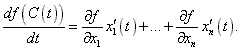
Ο κανόνας της αλυσίδας μπορεί να χρησιμοποιηθεί στην περίπτωση αλλαγής μεταβλητών, όπου δεν έχουμε μόνο μιά μεταβλητή, όπως φαίνεται στο παρακάτω παράδειγμα.

Παράδειγμα:  Έστω ότι η f είναι συνάρτηση των δύο μεταβλητών x, y και x = s(u, v), y = t(u, v), με s, t συναρτήσεις δύο μεταβλητών με τιμές στο R. Oρίζουμε g(u. v) = f(s(u, v), t(u, v)). Με την χρήση του κανόνα της αλυσίδας παίρνουμε

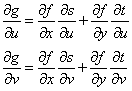
Ασκήσεις

1. Έστω Α, Β δύο διανύσματα. Αν g(t) = f(A+tB) να υπολογίσετε την παράγωγο της g.[Λύση]

2. Έστω f(x, y) = x²+xy  και C(t) = (t, t²). Nα υπολογίσετε την παράγωγο της f(C(t)) στο t=1.[Λύση]

3. Έστω f  μια διαφορίσιμη συνάρτηση στο R³  που ικανοποιεί f(tX) = tf(X) για κάθε πραγματικό t και κάθε ΧR³ . Να δείξετε ότι f(X) = gradf(0)·X.[Υπόδειξη]  [Λύση]

4. Έστω f  μια διαφορίσιμη συνάρτηση στο R²  που ικανοποιεί f(tX) = t^k f(X) για κάθε πραγματικό t και κάθε Χ=(x, y)R² όπου k ένας ακέραιος. Να δείξετε ότι

[Υπόδειξη]  [Λύση]

5. Έστω c μια σταθερά και z = f(x+ct) + g(x-ct), u=x+ct,  v=x-ct. Nα δείξετε ότι

[Λύση]

6. Έστω z = f(u, v),  u=x+y,  v=x-y.  Να δείξετε οτι

[Λύση]

[Περιεχόμενα]