KE
ΦΑΛΑΙΟ 10
ΤΟ ΕΠΙΦΑΝΕΙΑΚΟ ΟΛΟΚΛΗΡΩΜΑ
Έστω Φ(
u, v) η (λεία) παραμετρικοποίηση μιας επιφάνειας Σ, (u, v)![]()
Υποθέτουμε τώρα ότι η επιφάνεια περιέχεται σε ένα ανοικτό υποσύνολο Ζ του
R3 και F είναι ένα διανυσματικό πεδίο πάνω στο Ζ. Έστω n = n(u, v) το εξωτερικό μοναδιαίο κάθετο διάνυσμα στην επιφάνεια. Τότε το ολοκλήρωμα του διανυσματικού πεδίου F πάνω στην Σ είναι το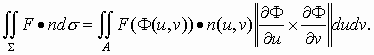
Ασκήσεις
1. Να υπολογίσετε το ολοκλήρωμα της συνάρτησης f(x, y, z) = x2 πάνω στην μοναδιαία σφαίρα. [Υπόδειξη] [Λύση]
2. Έστω Φ η παραμετρικοποίηση μιας επιφάνειας Σ:
Φ(
u, v) = (x(u, v), y(u, v), z(u, v)), (u, v)(ι) Αν
![]()
να δείξετε ότι το εμβαδόν της Σ είναι
![]()
Ποιό είναι το ολοκλήρωμα μιας συνάρτησης f πάνω στην Σ με την χρήση του παραπάνω τύπου;
(ιι) Πως γράφεται ο παραπάνω τύπος αν c = 0 ;
(ιιι) Να υπολογίσετε το εμβαδόν της επιφάνειας της σφαίρας ακτίνας 1 χρησιμοποιώντας τα (ι) και (ιι). [Λύση]