Έστω Α μια περιοχή στον R² με σύνορο μια κλειστή καμπύλη C : [a, b] ® R² θετικά προσανατολισμένη. Αν C(t) = (x(t), y(t)), το εξωτερικό κάθετο διάνυσμα στην C στο t είναι το

Θεώρημα της απόκλισης στον R²: Έστω Α, C, Ν όπως παραπάνω και F ένα C¹ διανυσματικό πεδίο στην Α. Τότε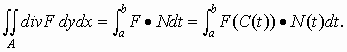

Yποθέτουμε τώρα ότι η Π είναι μια περιοχή στον R³ η οποία περικλείεται σε μια κλειστή και ομαλή (εκτός ίσως από ένα πεπερασμένο αριθμό από ομαλές καμπύλες) επιφάνεια Σ. και F ένα C¹ διανυσματικό πεδίο ορισμένο σε ένα ανοικτό σύνολο το οποίο περιέχει τις Σ, Π.

Θεώρημα της απόκλισης στον R³: Έστω Π, Σ, F όπως παραπάνω και n το εξωτερικό μοναδιαίο κάθετο διάνυσμα στην επιφάνεια Σ. Τότε

Ασκήσεις

1. Να υπολογισθεί το ολοκλήρωμα του δ.π. F(x, y, z) = (x², y², z) πάνω στην μοναδιαία σφαίρα. [Λύση]

2. Έστω f μια αρμονική συνάρτηση ορισμένη σε μια ανοικτή περιοχή που περιέχει τις Π, Σ, n το μοναδιαίο εξωτερικό κάθετο διάνυσμα στην επιφάνεια Σ και Df η παράγωγος της f στην κατεύθυνση του n. Nα αποδειχθεί ότι

   [Υπόδειξη] [Λύση]

3. Έστω f, g δύο συναρτήσεις ορισμένες σε μια ανοικτή περιοχή που περιέχει τις Π, Σ και n το μοναδιαίο εξωτερικό κάθετο διάνυσμα στην επιφάνεια Σ. Να αποδειχθούν οι τύποι του Green: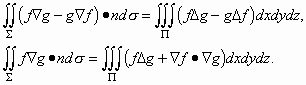

   [Λύση]

4. Έστω f μια αρμονική συνάρτηση ορισμένη στον δίσκο με κέντρο την αρχή και ακτίνα 1. Nα δειχθεί ότι για r(0, 1)

   [Υπόδειξη] [Λύση]

[Περιεχόμενα]