Δίνεται ένα διανυσματικό πεδίο F(x, y) = (p(x, y), q(x, y)) ορισμένο σε ένα ανοικτό υποσύνολο Α του επιπέδου, με p, q C¹ συναρτήσεις (δηλαδή με συνεχείς πρώτες μερικές παραγώγους). Έστω C : [a, b] ® A μιά καμπύλη στο Α. Γνωρίζουμε ότι

Υποθέτουμε ότι η καμπύλη είναι κλειστή (δηλαδή Α(a) = Α(b)), θετικά προσανατολισμένη (δηλαδή προσανατολισμένη αντίθετα προς την φορά των δεικτών του ρολογιού, συμβουλευθείτε το διδακτικό σας βιβλίο) και ο περιορισμός της Α στο (a, b) είναι 1-1. Έστω Π η περιοχή που περικλείει η καμπύλη.

Θεώρημα (Green): Έστω Α, Π, p, q όπως παραπάνω. Τότε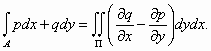

Παρατήρηση: Το παραπάνω θεώρημα ισχύει επίσης όταν η περιοχή Π έχει σαν σύνορο αντί της καμπύλης ένα κλειστό μονοπάτι που αποτελείται από ένα πεπερασμένο σύνολο από C¹ καμπύλες. Σ΄αυτή την περίπτωση θεωρούμε ότι αυτές οι καμπύλες είναι έτσι προσανατολισμένες ώστε το Π να ευρίσκεται αριστερά τους.

Aσκήσεις

όπου το μονοπάτι Α είναι το σύνορο του τετραγώνου με κορυφές (± 1, ± 1) θετικά προσανατολισμένο. [Λύση]

2. Υποθέτουμε ότι η συνάρτηση f ικανοποιεί την εξίσωση Laplace σε μία περιοχή Π η οποία περικλείεται σε μια καμπύλη Α θετικά προσανατολισμένη. Να υπολογίσετε το ολοκλήρωμα

   [Λύση]

3. Χρησιμοποιώντας το θεώρημα του Green να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται ανάμεσα σε ένα τόξο του κυκλοειδούς x = t – sint, y = 1 – cost, t[0, 2π], και στον άξονα των x. (Προσοχή: το t δεν είναι η γωνία μεταξύ του διανύσματος (x, y) και του άξονα των x). [Λύση]

[Περιεχόμενα]