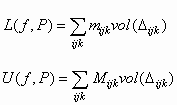
όπου
vol (Δijk) ο όγκος του Δijk.KE
ΦΑΛΑΙΟ 5
TO T
ΡΙΠΛΟ ΟΛΟΚΛΗΡΩΜΑ
Η διαδικασία ορισμού του τριπλού ολοκληρώματος
είναι όμοια με αυτήν του διπλού ολοκληρώματος. Ξεκινάμε με ένα ορθογώνιο παραλληλεπίπεδο Δ στο R3 :Δ
= [α, β]δηλαδή το σύνολο των σημείων
(x, y, z) στο R3 μεα £
x £ β, γ £ y £ δ, ε £ z £ ζ,και μια συνάρτηση
f : Δ ® R η οποία είναι φραγμένη στο Δ.Έστω Π
1 ={α = x0 < x1... < xn = β} μια διαμέριση του [α, β], Π2 = {γ = y0 < y1... < ym = δ} μια διαμέριση του [γ, δ] και Π3 ={ε = z0 < z1... < zs = ζ} μια διαμέριση του [ε, ζ]. Μια διαμέριση του Δ, συμβολιζόμενη με Ρ = Δ1Έστω m
ijk = inf{f(x, y, z) : (x, y, z)όπου 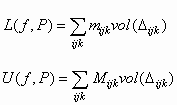
Η f θα λέγεται ολοκληρώσιμη στο Δ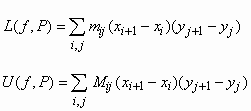
L(f, P) £ O £ U(f, Q)
για όλες τις διαμερίσεις
P, Q του Δ.Αν η f είναι ολοκληρώσιμη, ο αριθμός Ο θα λέγεται ολοκλήρωμα της f στο Δ και θα συμβολίζεται με
![]()
Στο διπλό ολοκλήρωμα είδαμε ότι αν η f είναι συνεχής στο Δ εκτός ίσως από ένα πεπερασμένο αριθμό από καμπύλες τότε είναι ολοκληρώσιμη. Στο τριπλό ολοκλήρωμα έχουμε το ίδιο αποτέλεσμα αν αντικαταστήσουμε τις καμπύλες με επιφάνειες. (δείτε τα θεωρήματα στο κεφάλαιο 2 [Mετάβαση στο κεφ. 2]).
Ομοίως
μπορούμε να υπολογίσουμε ένα τριπλό ολοκλήρωμα με την χρήση επάλληλων ολοκληρωμάτων:Θεώρημα:
Έστω γ, δ : [α, β] ® R δύο λείες συναρτήσεις τ.ω. γ(x) £ δ(x) ,xα
£ x £ β, γ(x) £ y £ δ(x).Έστω Α το σύνολο των σημείων (
x, y, z) στο R3 τ.ω.α
£ x £ β, γ(x) £ y £ δ(x) και ε(x) £ z £ ζ(x)και
f: A ® R μια συνεχής συνάρτηση. Τότε![]()
Ασκήσεις
1. Να υπολογίσετε το ολοκλήρωμα
με Δ = [0, 2] ![]() [0, 2]
[0, 2] ![]() [0, 2]. [Λύση]
[0, 2]. [Λύση]
2. Βρείτε τον όγκο της
περιοχής που περικλείεται μεταξύ τωνz = x2 + 3y2 και z = 12 – 2x2. [Λύση]
f μια συνεχής συνάρτηση, Βε η μπάλλα με κέντρο το σημείο (a, b, c) και ακτίνα ε > 0 και Vol(Βε) ο όγκος της. Να αποδείξετε ότι[Λύση]
4. Nα υπολογίσθεί ο όγκος της περιοχής που περικλείεται μεταξύ των
x2 + y2 = 2, x + y + z = 4, z = 0 . [Λύση]