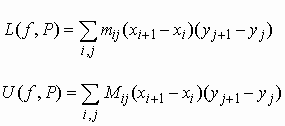
Η f θα λέγεται ολοκληρώσιμη στο Δ αν υπάρχει μοναδικός αριθμός Ο τ.ω.
ΚΕΦΑΛΑΙΟ 2
TO
ΔΙΠΛΟ ΟΛΟΚΛΗΡΩΜΑ
Έστω Δ το ορθογώνιο παραλληλόγραμμο
a £ x £ b, c £ y £ d στο επίπεδο και f : D ® R μια φραγμένη συνάρτηση (δηλαδή |f(x, y)| £ M για κάθε (x, y) στο Δ).Έστω Π
1 = {a = x0 ,x1,...,xk = b} μια διαμέριση του [a, b] και Π2 = {a = x0 ,x1,...,xs = b} μια διαμέριση του [c, d]. Το σύνολο των τετραγώνων [xi, xi+1]Έστω m
ij = inf{f(x, y) : xΗ f θα λέγεται ολοκληρώσιμη στο Δ αν
υπάρχει μοναδικός αριθμός Ο τ.ω.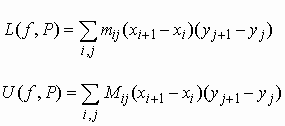
L(f, P) £ O £ U(f, Q)
για όλες τις διαμερίσεις
P, Q του Δ.Αν η f είναι ολοκληρώσιμη, ο αριθμός Ο θα λέγεται ολοκλήρωμα της f στο Δ και θα συμβολίζεται με
![]()
Θεώρημα 1: Αν η f είναι συνεχής στο Δ τότε είναι ολοκληρώσιμη στο Δ.
Μπορούμε να αποδείξουμε την παρακάτω γενίκευση του θεωρήματος 1.
Θεώρημα 2: Αν η f είναι φραγμένη και συνεχής στο Δ εκτός ίσως από τα σημεία που βρίσκονται πάνω σε ένα πεπερασμένο αριθμό από καμπύλες, τότε είναι ολοκληρώσιμη. [Mετάβαση στο κεφ. 5]
Θεώρημα 3: Έστω ότι οι f, g είναι ολοκληρώσιμες στο Δ και α, β είναι πραγματικοί. Τότε
1. Η αf + βg είναι ολοκληρώσιμη.
2.3. Αν f £ g τότε ([Επιστροφή] στην άσκηση 3 κεφ.5)
Διαδοχικά ολοκληρώματα
Θεώρημα
4: Έστω Δ = [a, b]![]()
υπάρχει, τότε
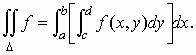
Έστω Α μια φραγμένη περιοχή στο επίπεδο, Δ ένα ορθογώνιο παραλληλόγραμμο που την περιέχει. και f μια συνάρτηση ορισμένη στην Α. Oρίζουμε
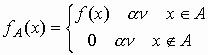
Έτσι, αν η fA είναι ολοκληρώσιμη στο Δ, μπορούμε να ορίσουμε το ολοκλήρωμα της f στο Α ως εξής:
![]()
Όταν η περιοχή Α περιγράφεται από τις ανισότητες
a £ x £ b , γ(x) £ y £ δ(x) με τις φ, δ λείες συναρτήσεις τότε έχουμε:Θεώρημα 5: Το ολοκλήρωμα μιας συνάρτησης
f στην παραπάνω περιοχή είναι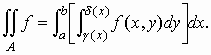
Ασκήσεις
1. Nα υπολογισθούν τα ολοκληρώματα
![]() [Λύση]
[Λύση]
2. Να υπολογισθεί το ολοκλήρωμα της συνάρτησης f(x, y) = x2y2 πάνω στην περιοχή Γ που περιγράφεται από την ανισότητα |x| + |y| £ 1. [Λύση]
3. Nα υπολογισθεί το εμβαδόν της περιοχής μεταξύ του άξονα των x και της y = x2 από x = 0 έως x = 1. [Λύση]