Έστω Σ μια επιφάνεια και Φ(u, v) μια παραμετρικοποίησή της με (u, v)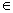A. Θα υποθέσουμε ότι η Σ είναι λεία και ότι η Φ είναι 1- 1.

Ορισμός: Tο εμβαδόν της Σ, το οποίο θα συμβολίζουμε με

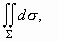
είναι το ολοκλήρωμα

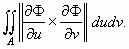
Εδώ με || || συμβολίζουμε την νόρμα στον R³.

Aσκήσεις

1. Υποθέτουμε ότι μια επιφάνεια Σ είναι το γράφημα της συνάρτησης z = f(x, y), (x, y)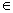A. Nα δείξετε ότι το εμβαδόν της Σ δίνεται από τον τύπο:

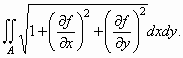   [Υπόδειξη] [Λύση]

2. Έστω Κ(t) = (x(t), z(t)), t 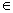[a, b], μια καμπύλη στο xz επίπεδο με x(t) ³ 0. Nα υπολογίσετε το εμβαδόν της επιφάνειας που προκύπτει όταν περιστρέψουμε την Κ γύρω από τον άξονα των z. Xρησιμοποιώντας το αποτέλεσμα να υπολογίσετε το εμβαδόν της επιφάνειας της σφαίρας ακτίνας 1. [Υπόδειξη] [Λύση]

3. Υποθέτουμε ότι μια επιφάνεια Σ η οποία είναι το γράφημα της συνάρτησης z = f(x, y), (x, y) 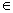A, περιγράφεται επίσης από την ισοσταθμική επιφάνεια {(x, y, z): F(x, y, z) = 0} της συνάρτησης F. Nα υπολογίσετε το εμβαδόν της Σ χρησιμοποιώντας μόνο την F. [Υπόδειξη] [Λύση]

[Περιεχόμενα]