


Next: Άσκηση 8
Up: Άσκηση 7
Previous: Υπόδειξη
Λύση
Η
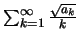 έχει θετικούς
όρους να δείξουμε οτι τα μερικά της αθροίσματα είναι ομοιόμορφα φραγμένα.
Έστω
έχει θετικούς
όρους να δείξουμε οτι τα μερικά της αθροίσματα είναι ομοιόμορφα φραγμένα.
Έστω
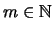 .
Από την ανισότητα Cauchy - Schwartz παίρνουμε
.
Από την ανισότητα Cauchy - Schwartz παίρνουμε
όπου
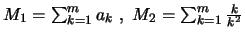 .
Έχουμε λοιπόν
.
Έχουμε λοιπόν 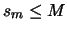 για κάθε
για κάθε
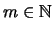 ,
όπου
,
όπου
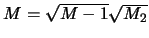 .
Έπεται οτι η
.
Έπεται οτι η
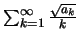 συγκλίνει.
συγκλίνει.
Άσκηση 7
Υπόδειξη
root
1999-07-29
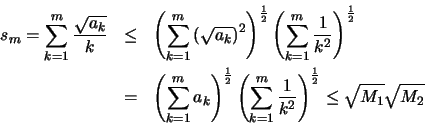
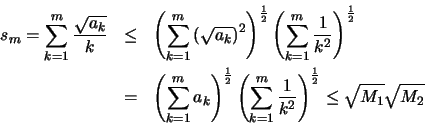
![]() .
Έχουμε λοιπόν
.
Έχουμε λοιπόν ![]() για κάθε
για κάθε
![]() ,
όπου
,
όπου
![]() .
Έπεται οτι η
.
Έπεται οτι η
![]() συγκλίνει.
συγκλίνει.