


Next: Άσκηση 2
Up: Άσκηση 1
Previous: Υπόδειξη
Λύση
Για 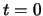 έχουμε
έχουμε
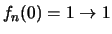 .
Αν
.
Αν ![$t\in (0,1]$](img768.gif) ,
τότε
,
τότε
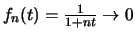 .
Άρα,
.
Άρα,
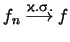 όπου
όπου
Κάθε 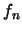 είναι συνεχής συνάρτηση. Αφού η
είναι συνεχής συνάρτηση. Αφού η 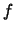 δεν είναι συνεχής, η σύγκλιση δεν μπορεί να
είναι ομοιόμορφη.
δεν είναι συνεχής, η σύγκλιση δεν μπορεί να
είναι ομοιόμορφη.
Απ'' ευθείας επιχείρημα: αν ήταν, τότε για 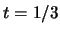 θα υπήρχε
θα υπήρχε
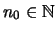 τέτοιο
ώστε για κάθε
τέτοιο
ώστε για κάθε
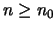 και
και 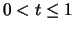 να ισχύει:
να ισχύει:
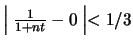 .
Δηλαδή
.
Δηλαδή
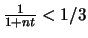 .
'Ομως για
.
'Ομως για 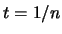 έχουμε
έχουμε
το οποίο είναι άτοπο.
Άσκηση 1
Υπόδειξη
root
1999-07-29
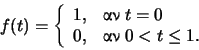
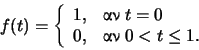
![]() θα υπήρχε
θα υπήρχε
![]() τέτοιο
ώστε για κάθε
τέτοιο
ώστε για κάθε
![]() και
και ![]() να ισχύει:
να ισχύει:
![]() .
Δηλαδή
.
Δηλαδή
![]() .
'Ομως για
.
'Ομως για ![]() έχουμε
έχουμε