


Next: Υπόδειξη
Up: Ακολουθίες συναρτήσεων
Previous: Λύση
Άσκηση 3
Έστω
![$f_n(t)=n^p t {(1-t^2)}^n \ ,\ t \in [0,1]$](img788.gif)
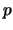 είναι παράμετρος στο
είναι παράμετρος στο 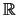 .
Αποδείξτε οτι, για κάθε
.
Αποδείξτε οτι, για κάθε
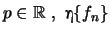 συγκλίνει κατά σημείο
σε κάποια
συγκλίνει κατά σημείο
σε κάποια 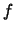 στο
στο ![$[0,1]$](img765.gif) .
Για ποιές τιμές του
.
Για ποιές τιμές του 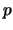 είναι η σύγκλιση ομοιόμορφη? Για ποιές τιμές του
είναι η σύγκλιση ομοιόμορφη? Για ποιές τιμές του 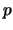 ισχύει οτι
ισχύει οτι
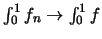 ?
?
Υπόδειξη
Λύση
root
1999-07-29