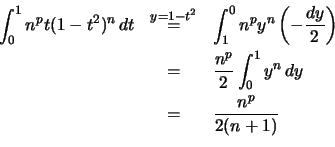Αν ![]() ,
τότε
,
τότε
![]() ,
άρα
,
άρα
![]() (δείξτε οτι
(δείξτε οτι
![]() ,
αν
,
αν ![]() ). Άρα, όποια και αν είναι η τιμή της παραμέτρου
). Άρα, όποια και αν είναι η τιμή της παραμέτρου
![]() ,
έχουμε
,
έχουμε
![]() ,
όπου
,
όπου ![]() η μηδενική συνάρτηση.
η μηδενική συνάρτηση.
Για να δούμε για ποιές τιμές του ![]() η σύγκλιση είναι ομοιόμορφη, βρίσκουμε τη μέγιστη τιμή της
η σύγκλιση είναι ομοιόμορφη, βρίσκουμε τη μέγιστη τιμή της
![]() :
:
![\begin{eqnarray*}
f_n^\prime (t) &=& n^p (1-t^2 )^n -n^p t (1-t^2 )^{n-1} (2t) \...
...} [1-t^2 -2nt^2 ] \\
&=& n^p (1- t^2 )^{n-1} [1-(2n+1)t^2 ]\\
\end{eqnarray*}](img799.gif)
Άρα, η ![]() έχει μέγιστο στο
έχει μέγιστο στο
![]() ,
ίσο με
,
ίσο με
Αν ![]() ,
τότε
,
τότε
Και στις δύο περιπτώσεις η σύγκλιση δεν είναι ομοιόμορφη.
Υπολογίζουμε το ολοκλήρωμα της ![]() :
: