Αν ![]() ,
τότε
,
τότε
![]() .
Αν
.
Αν ![]() ,
τότε
,
τότε
![]() (λόγω του
(λόγω του ![]() στο παρονομαστή). Για
να δείξουμε οτι η σύγκλιση είναι ομοιόμορφη στο
στο παρονομαστή). Για
να δείξουμε οτι η σύγκλιση είναι ομοιόμορφη στο ![]() ,
αρκεί να δείξουμε οτι
,
αρκεί να δείξουμε οτι
Δηλαδή, η μέγιστη τιμή της ![]() sto
sto ![]() είναι:
είναι:
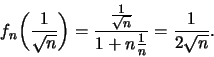
Αφού η ![]() είναι περιττή, έχουμε
είναι περιττή, έχουμε
![]() .
Άρα,
.
Άρα,
![]() .
.
Αν ![]() ,
τότε
,
τότε
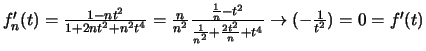 .
Αν
.
Αν
![]() .
.
Έστω ![]() διάστημα που δεν περιέχει το
διάστημα που δεν περιέχει το ![]() .
Έχουμε:
.
Έχουμε:
 στο
στο ![]() .
.
Αν το
![]() τότε
τότε
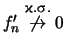 (αφού
(αφού
![]() ),
),
άρα
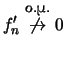 στο
στο ![]() .
.