


Next: Υπόδειξη
Up: Ακολουθίες συναρτήσεων
Previous: Λύση
Άσκηση 5
Έστω
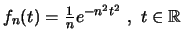 .
Αποδείξτε οτι
.
Αποδείξτε οτι
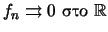 και
και
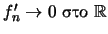 .
Αποδείξτε οτι
.
Αποδείξτε οτι
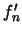 δεν συγκλίνει ομοιόμορφα στο
δεν συγκλίνει ομοιόμορφα στο 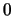 σε οποιοδήποτε διάστημα περιέχει το
σε οποιοδήποτε διάστημα περιέχει το
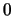 ,
ενώ
,
ενώ
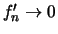 σε οποιοδήποτε κλειστό διάστημα δεν περιέχει το
σε οποιοδήποτε κλειστό διάστημα δεν περιέχει το 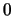 .
.
Υπόδειξη
Λύση
root
1999-07-29