


Next: Θεώρημα Weierstrass
Up: Άσκηση 5
Previous: Υπόδειξη
Λύση
Έχουμε
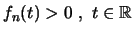 .
Παραγωγίζοντας, παίρνουμε
.
Παραγωγίζοντας, παίρνουμε
δηλαδή
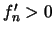 στο
στο 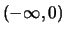 και
και
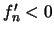 στο
στο 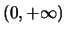 .
Άρα,
.
Άρα,
Έπεται οτι
Άρα,
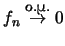 .
Έστω
.
Έστω
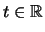 .
Είναι
.
Είναι
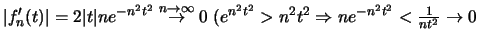 αν
αν 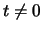 ,
και
,
και
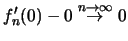 ).
Άρα,
).
Άρα,
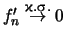 του
του 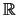 .
.
Αν ![$[\alpha , b]$](img379.gif) είναι ένα κλειστό διάστημα που δεν περιέχει στο
είναι ένα κλειστό διάστημα που δεν περιέχει στο 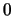 ,
τότε π.χ. αν
,
τότε π.χ. αν
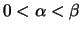 έχουμε
έχουμε
![$f^\prime _n (t)\vert
= 2\vert t\vert n e^{-n^2t^2} \leq 2bne^{-n^2\alpha ^2} \ \forall \ t \in [\alpha , b]$](img851.gif) και αφού
και αφού
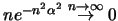 έπεται
οτι
έπεται
οτι
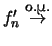 στο
στο ![$[\alpha , b]$](img379.gif) .
.
Άσκηση 5
Υπόδειξη
root
1999-07-29
![]() .
Παραγωγίζοντας, παίρνουμε
.
Παραγωγίζοντας, παίρνουμε ![]() είναι ένα κλειστό διάστημα που δεν περιέχει στο
είναι ένα κλειστό διάστημα που δεν περιέχει στο ![]() ,
τότε π.χ. αν
,
τότε π.χ. αν
![]() έχουμε
έχουμε
![]() και αφού
και αφού
![]() έπεται
οτι
έπεται
οτι
![]() στο
στο ![]() .
.