Next: Άσκηση 2
Up: Άσκηση 1
Previous: Υπόδειξη
Λύση
Η 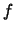 έχει την ακόλουθη ιδιότητα: αν
έχει την ακόλουθη ιδιότητα: αν
![$P:[0, 1] \rightarrow \mathbb R$](img864.gif) είναι οποιοδήποτε πολυώνυμο, τότε
είναι οποιοδήποτε πολυώνυμο, τότε
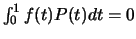 .
Πράγματι, αν
.
Πράγματι, αν
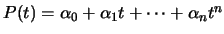 τότε από την υπόθεση
τότε από την υπόθεση
Έστω τώρα
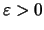 .
Υπάρχει πολυώνυμο
.
Υπάρχει πολυώνυμο
![$P:[0, 1] \rightarrow \mathbb R$](img864.gif) ώστε
ώστε
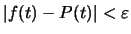 για κάθε
για κάθε ![$t\in [0, 1]$](img869.gif) .
Γράφουμε:
.
Γράφουμε:
Αφού το
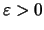 ήταν τυχόν, έπεται οτι
ήταν τυχόν, έπεται οτι
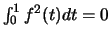 .
Αφού η
.
Αφού η 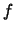 είναι συνεχής στο
είναι συνεχής στο ![$[0,1]$](img765.gif) ,
παίρνουμε
,
παίρνουμε 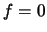 (γιατί ?)
(γιατί ?)
Άσκηση 1
Υπόδειξη
root
1999-07-29
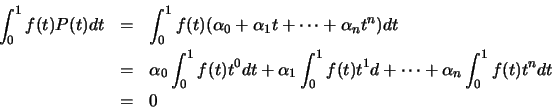
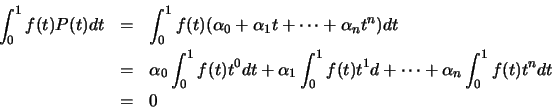
![]() .
Υπάρχει πολυώνυμο
.
Υπάρχει πολυώνυμο
![]() ώστε
ώστε
![]() για κάθε
για κάθε ![]() .
Γράφουμε:
.
Γράφουμε: