


Next: Άσκηση 4
Up: Άσκηση 3
Previous: Υπόδειξη
Λύση
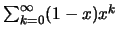 :
Υπολογίζουμε το μερικό άθροισμα
:
Υπολογίζουμε το μερικό άθροισμα
αν 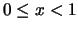 και
και 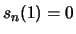 .
Άρα,
.
Άρα,
Αφού η 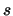 δεν είναι συνεχής στο
δεν είναι συνεχής στο 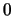 ,
η σύγκλιση δεν είναι ομοιόμορφη.
,
η σύγκλιση δεν είναι ομοιόμορφη.
Αν 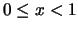 ,
τότε
,
τότε
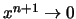 ,
άρα
,
άρα
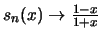 .
Αν
.
Αν 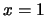 ,
τότε
,
τότε
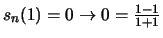 .
Άρα,
.
Άρα,
![$\sum ^\infty _{k=0} (-1)^kx^k(1-x)=\frac{1-x}{1+x}\ ,\ x\in [0, 1]$](img968.gif) .
Για να δείξουμε οτι η σύγκλιση είναι ομοιόμορφη, θεωρούμε την διαφορά
.
Για να δείξουμε οτι η σύγκλιση είναι ομοιόμορφη, θεωρούμε την διαφορά
Βρίσκουμε το
![$\max _{x\in [0, 1]} (x^{n+1}-x^{n+2}):$](img970.gif) η παράγωγος είναι
η παράγωγος είναι
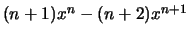 ,
άρα το μέγιστο πιάνεται στο
,
άρα το μέγιστο πιάνεται στο
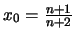 και είναι ίσο με
και είναι ίσο με
![$\left(\frac{n+1}{n+2}\right) ^{n+1} [1-\frac{n+1}{n+2}] < \frac{1}{n+2}$](img973.gif) .
.
Άρα,
Οπότε,
Άσκηση 3
Υπόδειξη
root
1999-07-29
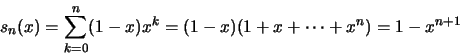
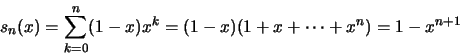
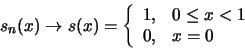
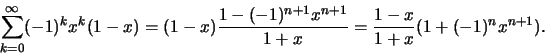
![]() η παράγωγος είναι
η παράγωγος είναι
![]() ,
άρα το μέγιστο πιάνεται στο
,
άρα το μέγιστο πιάνεται στο
![]() και είναι ίσο με
και είναι ίσο με
![]() .
.