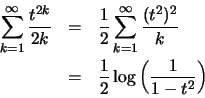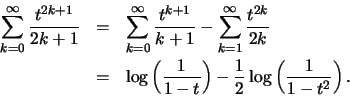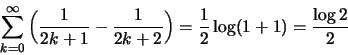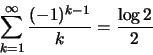(i) αν
Έστω ![]() .
Δείχνουμε οτι οι σειρές
.
Δείχνουμε οτι οι σειρές
![]() συγκλίνουν, χρησιμοποιώντας το κριτήριο του λόγου:
συγκλίνουν, χρησιμοποιώντας το κριτήριο του λόγου:
(i) αν
![]() ,
τότε
,
τότε
![]()
(ii) αν
![]() ,
τότε
,
τότε
![]()
Προσθέτοντας, βλέπουμε οτι η
![]() συγκλίνει
συγκλίνει
Αν ![]() ή
ή ![]() ,
είναι φανερό οτι η
,
είναι φανερό οτι η
![]() συγκλίνει (γιατί?). Άρα, η σειρά συγκλίνει κατά σημείο στο
συγκλίνει (γιατί?). Άρα, η σειρά συγκλίνει κατά σημείο στο ![]() .
.
Έχουμε δει οτι:
![]() ,
αν
,
αν ![]() .
Άρα,
.
Άρα,