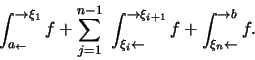Έστω πραγματική συνάρτηση ![]() ορισμένη σε διάστημα
ορισμένη σε διάστημα ![]() όπου
όπου
![]() και
και
![]() η
η ![]() .
Επιπλέον υποθέτουμε οτι για κάθε γ με
.
Επιπλέον υποθέτουμε οτι για κάθε γ με ![]() η
η ![]() είναι
είναι ![]() ολοκληρώσιμη στο
ολοκληρώσιμη στο ![]() .
Αν το όριο
.
Αν το όριο
![]() υπάρχει και είναι πραγματικός αριθμός τότε λέμε οτι η
υπάρχει και είναι πραγματικός αριθμός τότε λέμε οτι η ![]() έχει
γενικευμένο ολοκλήρωμα
στο
έχει
γενικευμένο ολοκλήρωμα
στο ![]() με τιμή ίση με
με τιμή ίση με