Πρόταση 55
(α) (Ολοκλήρωση κατά μέρη) Αν οι
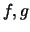
έχουν συνεχή παράγωγο στο
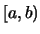
τότε
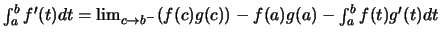
(β) (Αλλαγή μεταβλητής). Αν η
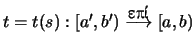
είναι γνησίως αύξουσα και έχει συνεχή παράγωγο
τότε
Ορισμός 56
Έστω συνάρτηση
![$f:[a, b)\cup(b, c] \rightarrow \mathbb R$](img1073.gif)
είναι
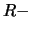
ολοκληρώσιμη σε
κάθε διάστημα
![$[a, d],\ a \leq d<b$](img1074.gif)
και σε κάθε διάστημα
![$[d, c],\ b<d \leq c$](img1075.gif)
.
Ονομάζουμε
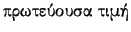
(principal value) του γενικευμένου ολοκληρώματος
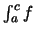
τον αριθμό (αν υπάρχει)
και τον συμβολίζουμε με
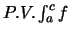
.
Είναι δυνατόν να μην υπάρχει το γενικευμένο ολοκλήρωμα αλλά να υπάρχει η πρωτεύουσα τιμή του. Για παράδειγμα, έστω
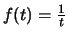
στο
![$[-1, 0) \cup (0, 1]$](img1080.gif)
.
Το γενικευμένο ολοκλήρωμα
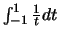
δεν υπάρχει αλλά
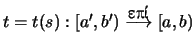 είναι γνησίως αύξουσα και έχει συνεχή παράγωγο
τότε
είναι γνησίως αύξουσα και έχει συνεχή παράγωγο
τότε