


Next: Άσκηση 3
Up: Άσκηση 2
Previous: Υπόδειξη
Λύση
(α)
Συνεχίζοντας με αυτόν τον τρόπο κατεβάζουμε συνεχώς τον εκθέτη του λογαρίθμου.
Αν κάνουμε ![$[q]+1$](img1136.gif) τέτοια βήματα (όταν
τέτοια βήματα (όταν 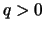 )
τότε προκύπτει οτι το
)
τότε προκύπτει οτι το
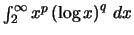 συγκλίνει αν και μόνο αν
το
συγκλίνει αν και μόνο αν
το
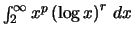 συγκλίνει με
συγκλίνει με 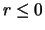 .
Όμως
.
Όμως 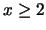 άρα
άρα
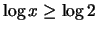 οπότε
οπότε
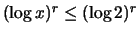 (αφού
(αφού 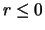 ).
Έτσι παίρνουμε
).
Έτσι παίρνουμε
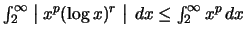 το οποίο συγκλινει για
το οποίο συγκλινει για 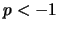 .
.
(β) Αν 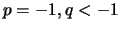 έχω το
έχω το
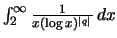 .
Θέτω
.
Θέτω
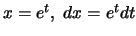 και το ολοκλήρωμα γίνετε
και το ολοκλήρωμα γίνετε
το οποίο συγκλίνει αν και μόνο αν 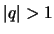 δηλαδή
δηλαδή 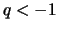 .
.
Άσκηση 2
Υπόδειξη
root
1999-07-29
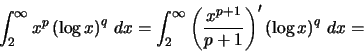
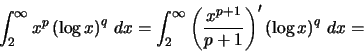
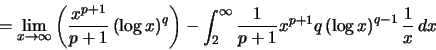
![]() έχω το
έχω το
![]() .
Θέτω
.
Θέτω
![]() και το ολοκλήρωμα γίνετε
και το ολοκλήρωμα γίνετε