


Next: Άσκηση 1
Up: Γενικευμένα ολοκληρώματα
Previous: Γενικευμένα ολοκληρώματα με παράμετρο
Έστω 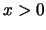 και ας θεωρήσουμε την συνάρτηση
και ας θεωρήσουμε την συνάρτηση
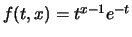 για
για 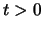 .
Σχηματίζουμε το γενικευμένο ολοκλήρωμα
.
Σχηματίζουμε το γενικευμένο ολοκλήρωμα
Έστω ορίζεται μια συνάρτηση του 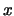 που συμβολίζουμε με
που συμβολίζουμε με 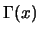 και ονομάζουμε
και ονομάζουμε
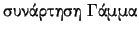 .
Αποδεικνύεται οτι το γενικευμένο αυτό ολοκλήρωμα συγκλίνει για κάθε
.
Αποδεικνύεται οτι το γενικευμένο αυτό ολοκλήρωμα συγκλίνει για κάθε 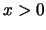 και συγκλίνει ομοιόμορφα σε κάθε διάστημα
και συγκλίνει ομοιόμορφα σε κάθε διάστημα ![$I=[A, B]$](img1110.gif) όπου
όπου
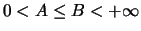 .
Η συνάρτηση
.
Η συνάρτηση 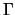 στο
στο 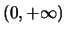 είναι άπειρες φορές παραγωγίσιμη και ισχύει
είναι άπειρες φορές παραγωγίσιμη και ισχύει
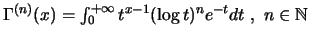 .
Επιπλέον ιδιότητες είναι οι εξής:
(α)
.
Επιπλέον ιδιότητες είναι οι εξής:
(α)
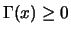 και
και
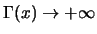 όταν
όταν
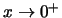 ή
ή
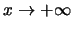
(β)
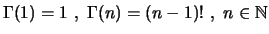
(γ)
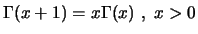
(δ) η  είναι κυρτή.
είναι κυρτή.
root
1999-07-29