


Next: Άσκηση 6
Up: Άσκηση 5
Previous: Υπόδειξη
Λύση
Έστω 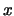 σημείο συσσώρευσης του
σημείο συσσώρευσης του  και έστω
και έστω
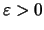 .
Ξέρουμε οτι
.
Ξέρουμε οτι
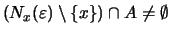 .
Ας υποθέσουμε οτι έχει πεπερασμένα το πλήθος στοιχεία, τα
.
Ας υποθέσουμε οτι έχει πεπερασμένα το πλήθος στοιχεία, τα
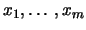 .
Είναι
.
Είναι
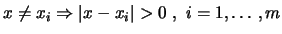 .
Θέτουμε
.
Θέτουμε
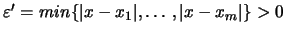 .
Τότε,
.
Τότε,
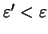 και
και
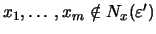 .
Δηλαδή,
.
Δηλαδή,
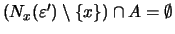 .
Άτοπο, γιατί το
.
Άτοπο, γιατί το 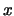 είναι σημείο συσσώρευσης του
είναι σημείο συσσώρευσης του  .
.
Δηλαδή,
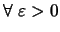 είναι
είναι
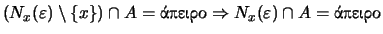 .
Το αντίστροφο είναι προφανές: αν κάθε περιοχή του
.
Το αντίστροφο είναι προφανές: αν κάθε περιοχή του 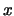 περιέχει άπειρα σημεία του
περιέχει άπειρα σημεία του  ,
τότε περιέχει και κάποιο διαφορετικό από το
,
τότε περιέχει και κάποιο διαφορετικό από το 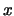 .
Δηλαδή για κάθε
.
Δηλαδή για κάθε
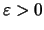 είναι
είναι
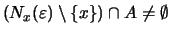 .
Αρα το
.
Αρα το 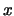 είναι σημείο συσσώρευσης του
είναι σημείο συσσώρευσης του  .
.
Άσκηση 5
Υπόδειξη
root
1999-07-29
![]() είναι
είναι
![]() .
Το αντίστροφο είναι προφανές: αν κάθε περιοχή του
.
Το αντίστροφο είναι προφανές: αν κάθε περιοχή του ![]() περιέχει άπειρα σημεία του
περιέχει άπειρα σημεία του ![]() ,
τότε περιέχει και κάποιο διαφορετικό από το
,
τότε περιέχει και κάποιο διαφορετικό από το ![]() .
Δηλαδή για κάθε
.
Δηλαδή για κάθε
![]() είναι
είναι
![]() .
Αρα το
.
Αρα το ![]() είναι σημείο συσσώρευσης του
είναι σημείο συσσώρευσης του ![]() .
.