


Next: Άσκηση 11
Up: Άσκηση 10
Previous: Υπόδειξη
Λύση
Έστω οτι η 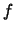 είναι συνεχής στο
είναι συνεχής στο 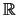 .
Ξέρουμε οτι η αντίστροφη εικόνα ανοικτού συνόλου είναι ανοικτό σύνολο, άρα το
.
Ξέρουμε οτι η αντίστροφη εικόνα ανοικτού συνόλου είναι ανοικτό σύνολο, άρα το
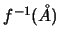 είναι ανοικτό. Αφού
είναι ανοικτό. Αφού
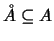 έχουμε
έχουμε
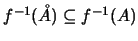 και αφού το
και αφού το
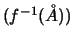 είναι το μεγαλύτερο ανοικτό σύνολο που περιέχεται στο
είναι το μεγαλύτερο ανοικτό σύνολο που περιέχεται στο 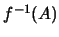 ,
έπεται στο
,
έπεται στο
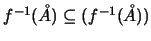 .
Αντίστροφα, αν η
.
Αντίστροφα, αν η
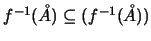 ισχύει για κάθε
ισχύει για κάθε
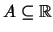 ανοικτό παίρνει τη μορφή
ανοικτό παίρνει τη μορφή
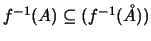 που σημαίνει οτι
που σημαίνει οτι
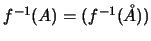 (γιατί ?). Αυτό πάλι σημαίνει οτι αντίστροφη εικόνα ανοικτού είναι ανοικτό, οπότε έχουμε δει οτι η
(γιατί ?). Αυτό πάλι σημαίνει οτι αντίστροφη εικόνα ανοικτού είναι ανοικτό, οπότε έχουμε δει οτι η 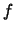 είναι συνεχής.
Έστω παλι οτι η
είναι συνεχής.
Έστω παλι οτι η 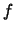 είναι συνεχής και
είναι συνεχής και
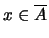 κάποιου
κάποιου
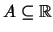 .
Υπάρχουν
.
Υπάρχουν 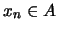 με
με
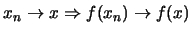 και
και
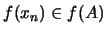 ,
άρα
,
άρα
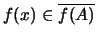 .
Δηλαδή,
.
Δηλαδή,
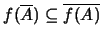 .
Αντίστροφα, έστω οτι ισχύει η
.
Αντίστροφα, έστω οτι ισχύει η
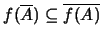 για κάθε
για κάθε
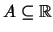 .
Θεωρούμε
.
Θεωρούμε
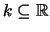 κλειστό και γράφουμε
κλειστό και γράφουμε 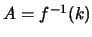 .
Τότε,
.
Τότε,
άρα
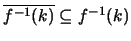 .
Αυτό σημαίνει οτι
.
Αυτό σημαίνει οτι 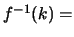 κλειστό. Αφού αντιστροφη εικόνα κλειστού είναι κλειστό, η
κλειστό. Αφού αντιστροφη εικόνα κλειστού είναι κλειστό, η 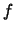 είναι συνεχής.
είναι συνεχής.
Άσκηση 10
Υπόδειξη
root
1999-07-29