


Next: Άσκηση 7
Up: Άσκηση 6
Previous: Υπόδειξη
Λύση
(α) Έχουμε
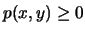 για κάθε
για κάθε 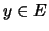 ,
άρα το
,
άρα το
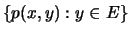 είναι κάτω φραγμένο από το
είναι κάτω φραγμένο από το 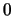 .
(Προφανές είναι μη-κενό, αφού υπάρχει τουλάχιστον ένα στοιχείο του
.
(Προφανές είναι μη-κενό, αφού υπάρχει τουλάχιστον ένα στοιχείο του 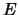 ). Έπεται από το αξίωμα της συνέχειας οτι υπάρχει το
). Έπεται από το αξίωμα της συνέχειας οτι υπάρχει το
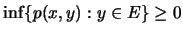 .
.
(β) Αν 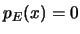 έχουμε οτι: για κάθε
έχουμε οτι: για κάθε
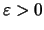 υπάρχει
υπάρχει
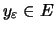 του
του
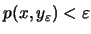 .
Παίρνοντας
.
Παίρνοντας
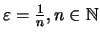 ,
ορίζουμε ακολουθία
,
ορίζουμε ακολουθία 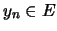 me
me
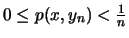 .
Έπεται οτι
.
Έπεται οτι
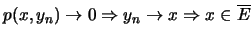 .
Αντίστροφα, αν
.
Αντίστροφα, αν
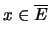 τότε για κάθε
τότε για κάθε
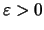 ισχύει
ισχύει
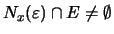 δηλαδή
δηλαδή
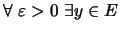 με
με
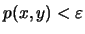 .
Έπεται οτι
.
Έπεται οτι
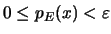 για κάθε
για κάθε
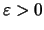 ,
δηλαδή
,
δηλαδή 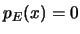 .
.
(γ) Έστω 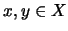 .
Αν
.
Αν 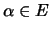 έχουμε
έχουμε
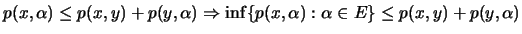 δηλαδή
δηλαδή
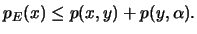 Έχουμε
Έχουμε
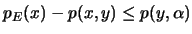 για κάθε
για κάθε 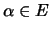 .
Άρα,
.
Άρα,
Δηλαδή,
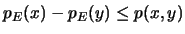 .
Από συμμετρία,
.
Από συμμετρία,
Η (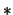 )
αποδεικνύει την συνέχεια της
)
αποδεικνύει την συνέχεια της 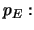 αν μας δώσουν
αν μας δώσουν 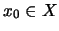 και
και
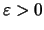 τότε για
τότε για
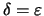 παίρνουμε: αν
παίρνουμε: αν
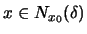 τότε
τότε
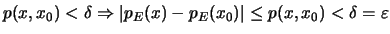 .
.
Άσκηση 6
Υπόδειξη
root
1999-07-29