


Next: Υπόδειξη
Up: Στοιχεία Θεωρίας
Previous: Λύση
Άσκηση 7
Ένας μετρικός χώρος 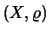 λέγεται διαχωρίσιμος αν υπάρχει υποσύνολό
του
λέγεται διαχωρίσιμος αν υπάρχει υποσύνολό
του  με τις ιδιότητες:
(α) το
με τις ιδιότητες:
(α) το  έχει αριθμήσιμο πλήθος στοιχείων και
έχει αριθμήσιμο πλήθος στοιχείων και
(β)
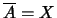 (δηλαδή το A είναι πυκνό στον
(δηλαδή το A είναι πυκνό στον 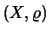 ).
Αποδείξτε οτι το
).
Αποδείξτε οτι το 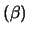 είναι ισοδύναμο με την
είναι ισοδύναμο με την
(β') οποιαδήποτε περιοχή
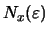 οποιουδήποτε σημείου
οποιουδήποτε σημείου
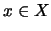 περιέχει στοιχείο του
περιέχει στοιχείο του  .
Είναι ο
.
Είναι ο 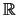 διαχωρίσιμος? Είναι ο
διαχωρίσιμος? Είναι ο
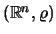 διαχωρίσιμος?
(Υπόδειξη: Θεωρείστε το σύνολο
διαχωρίσιμος?
(Υπόδειξη: Θεωρείστε το σύνολο  των σημείων που όλες τους οι συντεταγμένες είναι
ρητοί αριθμοί.)
Υπόδειξη
Λύση
των σημείων που όλες τους οι συντεταγμένες είναι
ρητοί αριθμοί.)
Υπόδειξη
Λύση
root
1999-07-29